\(f\left(x\right)=\left(m-4\right)x^2+\left(m+1\right)x+2m-1\)

\(f\left(x\right)< 0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m-4< 0\\\left(m+1\right)^2-4\left(m-4\right)\left(2m-1\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< 4\\m^2+2m+1-4\left(2m^2-m-8m+4\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow m^2+2m+1-8m^2+36m-16< 0\)

\(\Leftrightarrow-7m^2+38m-15< 0\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< 4\\\left[{}\begin{matrix}m< \dfrac{3}{7}\\m>5\end{matrix}\right.\end{matrix}\right.\)

\(KL:m\in\left(5;+\infty\right)\)

\(f\left(x\right)>0,\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a>0\\\Delta< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m+1>0\\\left[-2\left(m-1\right)\right]^2-4\left(m+1\right)\left(-m+4\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>-1\\4\left(m^2-2m+1\right)-4\left(-m^2+4m-m+4\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow4m^2-8m+4+4m^2-12m-16< 0\)

\(\Leftrightarrow8m^2-20m-12< 0\)

\(KL:m\in\left(-1;3\right)\)

Với $m=-1$ thì PT $f\left(x\right)=0$ có nghiệm $x=1$ (chọn)

Với $m\ne -1$ thì $f\left(x\right)$ là đa thức bậc 2 ẩn $x$

$f\left(x\right)=0$ có nghiệm khi mà ${}^{}={}^{}-2m(m+1)\ge 0$

$\iff -{}^{}-2m\ge 0\iff m(m+2)\le 0$

$\iff -2\le m\le 0$

Tóm lại để $f\left(x\right)=0$ có nghiệm thì $m\in [-2;0]$

Do \(a=1>0\) nên \(f\left(x\right)\ge0;\forall x\) khi:

\(\Delta'=\left(m-3\right)^2-4m\le0\)

\(\Leftrightarrow m^2-10m+9\le0\)

\(\Rightarrow1\le m\le9\)

Tìm m để f(x) < 0 vô nghiệm

⇔ f(x) ≥ 0 ∀ x ∈ R

⇔ Δ' ≤ 0

⇔ m² - 3m - 4 ≤ 0

⇔ -1 ≤ m ≤ 4

Vậy bpt có nghiệm khi \(\left[{}\begin{matrix}m< -1\\m>4\end{matrix}\right.\)

f(x) = (m + 1) x 2  - 2(3 - 2m)x + m + 1 ≥ 0 (1)

Với m = -1:

(1) ⇔ -10x ≥ 0 ⇔ x ≤ 0

Vậy với m = -1 bất phương trình (1) có nghiệm x ≤ 0

Suy ra, m = -1 (loại)

Với m ≠ -1:

f(x) = (m +1 ) x 2  - 2(3 - 2m)x + m + 1

Δ' = [-(3 - 2m) ] 2  - (m + 1)(m + 1) = (2m - 3 ) 2  - (m + 1 ) 2

= (2m - 3 + m + 1)(2m - 3 - m - 1) = (3m - 2)(m - 4)

Để bất phương trình (1) vô nghiệm thì:

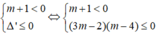
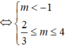
Vậy không có giá trị nào của m để bất phương trình (1) vô nghiệm

f(x) = (m-2) x 2  - 2mx + m + 1 > 0 (*)

Với m = 2 thì bất phương trình (*) trở thành:

f(x) = -4x + 3 > 0 ⇔ x < 3/4

Vậy với m = 2 thì bất phương trình (*) có nghiệm x < 3/4 nên m = 2 (loại)

Với m ≠ 2 thì bất phương trình (*) vô nghiệm khi và chỉ khi

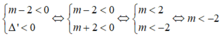
Vậy với m < -2 thì bất phương trình (*) vô nghiệm

ĐKXĐ: \(x\ge0\)

\(\left(x^2-x-m\right)\sqrt{x}=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)

Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm

Do đó:

a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm 

\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)

b. Để pt có 2 nghiệm pb 

TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0

\(\Leftrightarrow m=0\)

TH2: (1) có 2 nghiệm trái dấu

\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)

\(\Rightarrow m\ge0\)

c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)