Tìm min max của hàm số
y =-2x² +x-3 trên [-4;2]
Những câu hỏi liên quan
2 tháng 3 2021 lúc 14:18
Tìm Max của hàm số
y = f(x) = \(\left|\dfrac{2x^2+x-1}{x^2-x+1}\right|\)
Xét \(g\left(x\right)=\dfrac{2x^2+x-1}{x^2-x+1}\)
\(g\left(x\right)=\dfrac{3x^2-\left(x^2-x+1\right)}{x^2-x+1}=\dfrac{3x^2}{x^2-x+1}-1\ge-1\)
\(g\left(x\right)=\dfrac{3\left(x^2-x+1\right)-x^2+4x-4}{x^2-x+1}=3-\dfrac{\left(x-2\right)^2}{x^2-x+1}\le3\)
\(\Rightarrow-1\le g\left(x\right)\le3\Rightarrow0\le\left|g\left(x\right)\right|\le3\)
\(\Rightarrow y_{max}=3\) khi \(x=2\)
Đúng 1
Bình luận (0)
24 tháng 1 2021 lúc 5:54
Tìm Min và Max của hàm số sau trên R
y = f(x) =\(\sqrt{3x}+\sqrt{10-2x}\)
tìm tập xác định của hàm số
y=\(\dfrac{1}{x^{4^{ }}-2x^{2^{ }}+3}\)
ĐKXĐ:
\(x^4-2x^2+3\ne0\)
\(\Leftrightarrow\left(x^2-1\right)^2+2\ne0\) (luôn đúng)
Hàm xác định trên R hay \(D=R\)
Đúng 0
Bình luận (0)
Tìm GTLN (max); GTNN (min) của hàm số
y
2
x
+
1
+
4
-
x
.
Đọc tiếp
Tìm GTLN (max); GTNN (min) của hàm số y = 2 x + 1 + 4 - x .
Tìm GTLN (max), GTNN (min) của hàm số
y
x
+
2
x
với
x
∈
1
;
3
Đọc tiếp
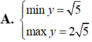
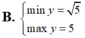
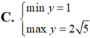
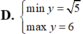
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x với x ∈ 1 ; 3
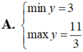
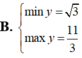
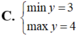
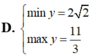
mn cho tui hỏi cái
tìm min max của |f(x)| ý
sao Max lại tìm theo 2TH còn min lại tìm theo so sánh trên dưới với trục ox vậy
tai sao lại không thể làm theo cách của tìm max
dạng mà tìm tham số m để hàm số |f(x)| có Min/Max trên [a,b] ý
tìm tập xác định của hàm số
y=√|2x−4|
Tìm GTLN (max), GTNN (min) của hàm số
y
x
+
2
x
2
+
1
trên
-
1
;
1
Đọc tiếp
Tìm GTLN (max), GTNN (min) của hàm số y = x + 2 x 2 + 1 trên - 1 ; 1
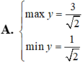
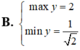
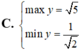
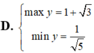
tìm tập xác định của hàm số
y=\(\sqrt{\left|2x-4\right|}\)