cho tam giác ABC vuông tại A có cạnh AB=3 , AC = \(\sqrt{3}\),BC= \(\sqrt{12}\),kẻ AH vuông góc BC .Tính AH,BH,HC

Những câu hỏi liên quan
Mình đang cần gấp bài này. Mong các bạn giúp mình nhé. Cảm ơn các bạn
Bài 3: Cho tam giác ABC vuông tại A có AC=20cm. Kẻ AH vuông góc với BC. Biết BH=9cm,HC=16cm. Tính độ dài cạnh AB, AH?
Bài 6: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH=2cm,AB=4cm. Tính chu vi tam giác ABC.
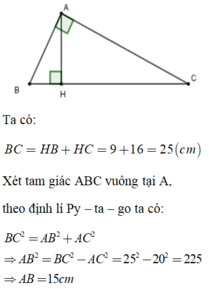
Bài 3 :
\(BC=HC+HB=16+9=25\left(cm\right)\)
\(BC^2=AB^2+AC^2\Rightarrow AB^2=BC^2-AC^2=25^2-20^2=625-400=225=15^2\)
\(\Rightarrow AB=15\left(cm\right)\)
\(AH^2=HC.HB=16.9=4^2.3^2\Rightarrow AH=3.4=12\left(cm\right)\)
Bài 6:
\(AB=AC=4\left(cm\right)\) (Δ ABC cân tại A)
\(BH=HC=2\left(cm\right)\) (Ah là đường cao, đường trung tuyến cân Δ ABC)
\(BC=BH+HC=2+2=4\left(cm\right)\)
Chu vi Δ ABC :
\(4+4+4=12\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, kẻ HE vuông góc với AB (E thuộc AB), kẻ HF vuông góc với AC (F thuộc AC)
a, Chứng minh AE . AB = AF. AC = BH . HC
b, Cho AB =\(\sqrt{12}\) cm, HC = 4cm. Tính AB, BC
c, AE . EB + AF . FC = BH . HC
d, AH\(^3\) = BC. HE. HF
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\left(1\right)\)
Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AH^2=AE\cdot AB\left(2\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AH^2=AF\cdot AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AF\cdot AC=BH\cdot HC\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AC 20 cm. Kẻ AH vuông góc với BC. Biết BH 9cm, HC 16 cm. Tính độ dài cạnh AB, AH? A.
A
H
12
c
m
;
A
B
15
c
m
B.
A
H
10
c
m
;
A
B
15
c
m
C.
A
H
15
c
m
;
A...
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 20 cm. Kẻ AH vuông góc với BC. Biết BH = 9cm, HC = 16 cm. Tính độ dài cạnh AB, AH?
A. A H = 12 c m ; A B = 15 c m
B. A H = 10 c m ; A B = 15 c m
C. A H = 15 c m ; A B = 12 c m
D. A H = 12 c m ; A B = 13 c m
Cho tam giác ABC vuông tại A có AB=6cm,AC=8 cm . Kẻ AH vuông góc BC . Tính BC, AH,BH,HC
Ap dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Đúng 0
Bình luận (0)
Ta có hình vẽ:
Áp dụng định lý Pitago. Ta có:
BC2 = AB2 + AC2 <=> 62 + 82 = 100 cm2
100 = 10 x 10
=> BC = 10 cm
Áp dụng công thức Heron để tính chiều cao. Ta có:
\(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (p là chu vi, S là diện tích, a,b,c là độ dài 3 cạnh)
Ta có: Chu vi tam giác là: 6 + 8 + 10 =24 cm
Vậy \(S=\sqrt{24\left(24-6\right)\left(24-8\right)\left(24-10\right)}=48\sqrt{42}\)
Để tính chiều cao AH, ta lấy 2 lần diện tích chia cho đáy ( BC) sẽ có được chiều cao
2 lần diện tích là: \(48\sqrt{42}.2=96\sqrt{42}\)
\(\Rightarrow AH=96\sqrt{42}:10=\frac{24\sqrt{42}}{25}\)
Độ dài cạnh BH là: (Bạn tự làm)
Độ dài cạnh HC là: (Bạn tự làm nhé)
Đúng 0
Bình luận (0)
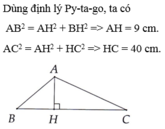
cho tam giác ABC có góc BAC>90 độ . Kẻ AH vuông góc BC tại H. Biết AB=15 cm, AC=41 cm, BH=12 cm . Tính độ dài cạnh HC
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)
Đúng 1
Bình luận (0)
1, Tam giác ABC vuông tại A, kẻ đường cao AH
a.Tính AB, AC,BC, HC nếu AH= 6cm, BH= 4,5cm
b.Biết AB= 6cm, HB- 3cm. Tính AH, AC,CH
5, Cho tam giác ABC vuông tại A có AB=21cm, góc C= 40 độ
a.Tính AC
b,Tính BC
Bài 5:
a) Xét ΔABC vuông tại A có
\(AC=AB\cdot\cot\widehat{C}\)
\(=21\cdot\cot40^0\)
\(\simeq25,03\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+25,03^2=1067,5009\)
hay \(BC\simeq32,67\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có B A C ^ > 90 ° . Kẻ AH vuông góc với BC tại H. Biết AB = 15 cm; AC = 41 cm, BH = 12 cm. Tính độ dài cạnh HC.
Cho tam giác ABC cân tại A có AB = AC = 5cm, kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh: BH = HC và góc BAH = góc CAH
b) Tính độ dài BH biết AH = 4cm.
c) Kẻ HD vuông góc với AB (D thuộc AB), kẻ EH vuông góc với AC (E thuộc AC). Tam giác ADE là tam giác gì ? Vì sao ?
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A tính BH,CH, AC ,AH biết:1, AB 12 cm BC 13cm AB 5 cm BC 1dmAB 3sqrt{3} cm BC 9cm2,Tính BC ,AH, BH ,CHAB 24 cm AC 18cmAB 2sqrt{2} cm AC 2sqrt{2}cmAB 3sqrt{3} cm AC 9cm
Đọc tiếp
Cho tam giác ABC vuông tại A tính BH,CH, AC ,AH biết:
1, AB =12 cm BC= 13cm
AB =5 cm BC= 1dm
AB =3\(\sqrt{3}\) cm BC= 9cm
2,Tính BC ,AH, BH ,CH
AB =24 cm AC= 18cm
AB =2\(\sqrt{2}\) cm AC= 2\(\sqrt{2}\)cm
AB =3\(\sqrt{3}\) cm AC= 9cm