xác định tính liên tục của hàm số trên r
f(x)=2sinx+3tan2x
Những câu hỏi liên quan
Xét tính liên tục của hàm số sau trên tập xác định của nó:
f
(
x
)
x
2
-
5
x
+
6
k
h
i
x
3...
Đọc tiếp
Xét tính liên tục của hàm số sau trên tập xác định của nó: f ( x ) = x 2 - 5 x + 6 k h i x > 3 2 x + 1 k h i x ≤ 3
Xét tính liên tục của hàm số sau trên tập xác định của nó:
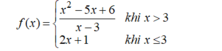
● Hàm số liên tục với mọi x ≠ 3.
● Tại x = 3, ta có:
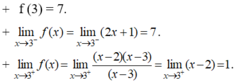
⇒ Hàm số không liên tục tại x = 3.
- Vậy hàm số liên tục trên các khoảng (-∞ ; 3), (3 ; +∞).
Đúng 0
Bình luận (0)
Xét tính liên tục của hàm số
f
(
x
)
x
2
+
5
x
+...
Đọc tiếp
Xét tính liên tục của hàm số f ( x ) = x 2 + 5 x + 4 x 3 + 1 n ế u x ≠ - 1 1 n ế u x = 1 trên tập xác định của nó.
Cho hàm số yf(x) xác định và liên tục trên R. Đồ thị của hàm số yf(x) hình trên. Kết luận nào sau đây về tính đơn điệu của hàm số
y
f
x
−
2
x
+
2018
là đúng? A. Hàm số đồng biến trên R B. Hàm số đồng biến trên các khoảng
−
∞
;
0
C. Hàm số đồng biến trên khoảng ...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên R. Đồ thị của hàm số y=f'(x) hình trên. Kết luận nào sau đây về tính đơn điệu của hàm số y = f x − 2 x + 2018 là đúng?
A. Hàm số đồng biến trên R
B. Hàm số đồng biến trên các khoảng − ∞ ; 0
C. Hàm số đồng biến trên khoảng 1 ; + ∞
D. Hàm số nghịch biến trên khoảng − 1 ; 5
Đáp án C
Ta có y ' = f ' x − 2 dựa trên đồ thị ta thấy x ∈ 1 ; + ∞ ⇒ f ' x > 2 ⇒ f ' x − 2 > 0 ⇒ y đồng biến
Đúng 0
Bình luận (0)
Xét tính liên tục của các hàm số sau trên tập xác định của chúng
f
(
x
)
x
2
-
2
x
-...
Đọc tiếp
Xét tính liên tục của các hàm số sau trên tập xác định của chúng f ( x ) = x 2 - 2 x - 2 n ế u x ≠ 2 2 2 n ế u x = 2
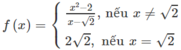
Tập xác định của hàm số là D = R
- Nếu x ≠ √2 thì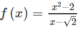 
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng (-∞; √2) và (√2; +∞)
- Tại x = √2:
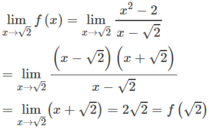
Vậy hàm số liên tục tại x = √2
Kết luận : y = f(x) liên tục trên R
Đúng 0
Bình luận (0)
Xét tính liên tục của các hàm số sau trên tập xác định của chúng
g
(
x
)
1
-
x
x
-...
Đọc tiếp
Xét tính liên tục của các hàm số sau trên tập xác định của chúng g ( x ) = 1 - x x - 2 2 n ế u x ≠ 2 3 n ế u x = 2
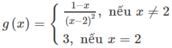
có tập xác định là D = R
- Nếu x ≠ 2 thì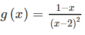 
là hàm phân thức hữu tỉ, nên nó liên tục trên các khoảng (-∞; 2) và (2; +∞)
Tại x = 2: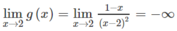 
Vậy hàm số y = g(x) không liên tục tại x = 2
Kết luận: y = g(x) liên tục trên các khoảng (-∞; 2) và (2; +∞) nhưng gián đoạn tại x = 2
Đúng 0
Bình luận (0)
Cho hàm số
f
x
3
x
+
2
n
ế
u
x
-
1...
Đọc tiếp
Cho hàm số f x = 3 x + 2 n ế u x < - 1 x 2 - 1 n ế u x ≥ - 1
a. Vẽ đồ thị hàm số y= f(x). Từ đó nêu nhận xét vê tính liên tục của hàm số trên tập xác định của nó.
b. Khẳng định nhận xét trên bằng 1 chứng minh.
a) Đồ thị hàm số (hình bên).
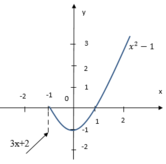
Quan sát đồ thị nhận thấy :
+ f(x) liên tục trên các khoảng (-∞ ; -1) và (-1 ; ∞).
+ f(x) không liên tục tại x = -1.
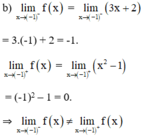
⇒ không tồn tại giới hạn của f(x) tại x = -1.
⇒ Hàm số không liên tục tại x = -1.
Đúng 0
Bình luận (0)
Cho hàm số yf(x) xác định và liên tục trên R, có đạo hàm f’(x). Biết rằng đồ thị hàm số f’(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)f(x) +x . A. Không có giá trị B. x 0 C. x 1 D. x 2
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên R, có đạo hàm f’(x). Biết rằng đồ thị hàm số f’(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)=f(x) +x .
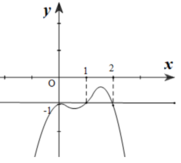
A. Không có giá trị
B. x = 0
C. x = 1
D. x = 2
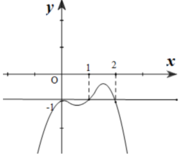
Cho hàm số yf(x) xác định và liên tục trên R, có đạo hàm f(x). Biết rằng đồ thị hàm số f(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)f(x)+x. A. Không có giá trị
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên R, có đạo hàm f'(x). Biết rằng đồ thị hàm số f'(x) như hình vẽ. Xác định điểm cực đại của hàm số g(x)=f(x)+x.
A. Không có giá trị
trang 77 SGK Toán 11 tập 1 - Cánh Diều
14 tháng 7 2023 lúc 9:45
Xét tính liên tục của mỗi hàm số sau trên tập xác định của hàm số đó:
a) f(x)=x2+sinx;
b) g(x)=x4−x2+\(\dfrac{6}{x-1}\);
c) h(x)=`(2x)/(x−3)+(x−1)/(x+4)`.
a: TXĐ: D=R
x^2;sin x đều liên tục trên R
=>f(x) liên tục trên R
b: TXĐ: D=R\{1}
x^4;-x^2;6/x-1 đều liên tục khi x thuộc (-vô cực;1) hoặc (1;+vô cực)
=>g(x) liên tục trên (-vô cực;1) và (1;+vô cực)
c: ĐKXĐ: x<>3; x<>-4
HS \(\dfrac{2x}{x-3}\) liên tục trên (-vô cực;3) và (3;+vô cực)
(x-1)/(x+4) liên tục trên (-vô cực;-4) và (-4;+vô cực)
=>h(x) liên tục trên từng khoảng xác định của nó
Đúng 0
Bình luận (0)