Cho tam giác ABC vuông tại a hãy viết các tỉ số lượng giác của b rồi suy ra tỉ số lượng giác góc C

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB =3cm,AC =4cm hãy tính tỉ số lượng giác của góc c rồi suy ra tỉ số lượng giác của góc b
Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{4}{5}\\ \cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{3}{5}\\ \tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{4}{3}\\ \cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{3}{4}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại C, có AC = 0,8 cm, BC = 0,9 cm. Hãy tính tỉ số lượng giác góc B, rồi suy ra tỉ số lượng giác của góc A
cho tam giác ABC vuông tại A. Biết AB=4cm;BC=5cm.tính tỉ số lượng giác của góc B rồi suy ra tỉ số lượng giác góc C ?
\(AC=\sqrt{BC^2-AB^2}=4\left(cm\right)\left(pytago\right)\\ \sin\widehat{B}=\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{4}{5}\\ \cos\widehat{B}=\sin\widehat{C}=\dfrac{AB}{AC}=\dfrac{3}{5}\\ \tan\widehat{B}=\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{4}{3}\\ \cot\widehat{B}=\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{3}{4}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB=3cm; AC=4cm
a)Tính BC
b)Vẽ AH vuông góc BC. TÍnh AH,BH,CH
c)Vẽ AD là phân giác góc BAC. Tính BD,DC
d)viết tỉ số lượng giác của góc B rồi suy ra tỉ số lượng giác góc C
a: Xét ΔBAC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=5(cm)
b: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2,4\left(cm\right)\\BH=1,8\left(cm\right)\\CH=3,2\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, AB = 6cm, AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C.
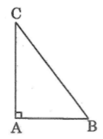
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100
Suy ra: BC = 10 (cm)
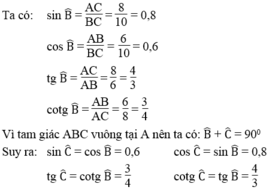
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại C , AC =0,9cm,BC =1,2 cm .Tính các tỉ số lượng giác của góc B , từ đó suy ra các tỉ số lượng giác của góc A
Áp dụng định lý Pitago:
\(AB=\sqrt{AC^2+BC^2}=1,5\left(cm\right)\)
\(sinB=\dfrac{AC}{AB}=0,6\) \(\Rightarrow cosA=sinB=0,6\)
\(cosB=\dfrac{BC}{AB}=0,8\) \(\Rightarrow sinA=cosB=0,8\)
\(tanB=\dfrac{AC}{BC}=\dfrac{3}{4}\) \(\Rightarrow cotA=tanB=\dfrac{3}{4}\)
\(cotB=\dfrac{BC}{AB}=\dfrac{4}{3}\) \(\Rightarrow tanA=cotB=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Tính các tỉ số lượng giác của góc B, từ đó suy ra các tỉ số lượng giác của góc C
\(BC^2=AB^2+AC^2=36+64=100=10^2\)
\(\Rightarrow BC=10\left(cm\right)\)
\(SinB=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\Rightarrow SinC=Sin\left(90-B\right)=CosB=\dfrac{3}{5}\)
\(CosB=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\Rightarrow CosC=Cos\left(90-B\right)=SinB=\dfrac{4}{5}\)
\(tanB=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\Rightarrow tanC=tan\left(90-B\right)=CotB=\dfrac{3}{4}\)
\(CotB=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\Rightarrow cotC=cot\left(90-B\right)=tanB=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 60mm, AC = 8cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Đổi AB=60mm=6cm
Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có
\(\left\{{}\begin{matrix}\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\\\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\\\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\\\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\\\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{8}{10}=\dfrac{4}{5}\\\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\\\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 1,6cm, AC = 1,2cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc C
Cho tam giác ABC vuông tại C có BC = 1,2cm, AC = 0,9cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A
Sử dụng các tỉ số lượng giác, tính được:
sinB = 3 5 ; cosB = 4 5 ; tanB = 3 4 ; cotB = 4 3
=> sinA = 4 5 ; cosA = 3 5 ; tanA = 4 3 ; cotA = 3 4
Đúng 0
Bình luận (0)

















