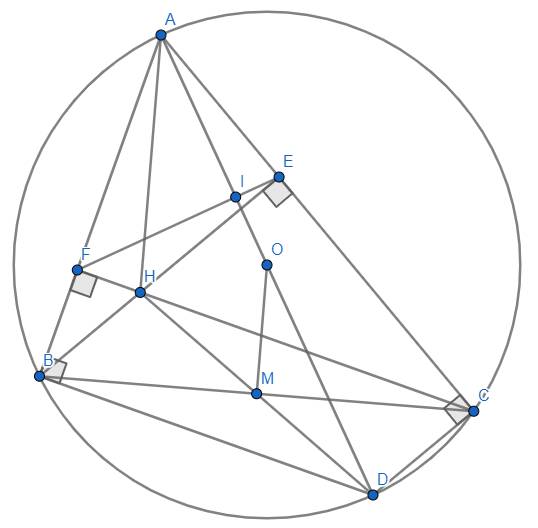
△ABC nội tiếp đường tròn đường kính AD, M(3;-1) là trung điểm BC, Đường cao kẻ từ B của △ABC đi qua E(-1;-3), điểm F(1;3) nằm trên đường thẳng AC. Tìm tọa độ đỉnh A và viết phương trình cạnh BC biết D(4;-2)

Những câu hỏi liên quan
Cho tam giác nhọn ABC AB < BC< AC nội tiếp trong đường tròn (O), Kẻ đường cao AD, BE, CF cắt nhau tại H.
1. Chứng minh tứ giác CDHE nội tiếp đường tròn đường kính HC
2. Đường tròn (K) đường kính HC cắt đường tròn (O) ở M ( M khác C). B< cắt đường tròn (K) ở N. Chứng minh BD.BC = BN.BM
3. CM AB// EN
4. 3 điểm N,D, F thẳng hàng
1) Cho Δ ABC nội tiếp đường tròn (O), 3 đường cao AD, BE, CK cắt nhau tại H.
a) C/m: BKHD nội tiếp; BKEC nội tiếp; AKHE nội tiếp.
b) Vẽ đường kính AM. C/m: BH // CM suy ra BHCM là hình bình hành.
cho tam giác ABC nhọn có ABAC nội tiếp đường tròn tâm O , bán kính R . gọi H là giao điểm của 3 đường cao AD,BE,CF của tam giác ABC . kẻ đường kính AK của đường tròn (O) , AD cắt (O) tại điểm N1. chứng minh AEDB , AEHF là tứ giác nội tiếp và AB.AC2R.AD2. chứng minh HK đi qua tring điểm M của BC3. gọi bán kính đường tròn ngoại tiếp tứ giác AEHF là r . chứng minh OM^2R^2-r^24. chứng minh OC vuông góc với DE và N đối xứng với H qua đường thẳng BC
Đọc tiếp
cho tam giác ABC nhọn có AB<AC nội tiếp đường tròn tâm O , bán kính R . gọi H là giao điểm của 3 đường cao AD,BE,CF của tam giác ABC . kẻ đường kính AK của đường tròn (O) , AD cắt (O) tại điểm N
1. chứng minh AEDB , AEHF là tứ giác nội tiếp và AB.AC=2R.AD
2. chứng minh HK đi qua tring điểm M của BC
3. gọi bán kính đường tròn ngoại tiếp tứ giác AEHF là r . chứng minh OM^2=R^2-r^2
4. chứng minh OC vuông góc với DE và N đối xứng với H qua đường thẳng BC
Cho ∆ ABC nhọn nội tiếp đường tròn (O;R)(AB<AC) có các đường cao AD và BE cắt nhau tại H. Gọi M là trung điểm BC . Đường tròn (K) đường kính AH cắt AM tại P. Gọi R' là bán kính đường tròn ngoại tiếp tam giác BPC
Cmr tứ giác HDMP nội tiếp được đường tròn
Vì \(P\in\left(K\right)\Rightarrow\angle APH=90\Rightarrow\angle APH=\angle ADM=90\Rightarrow HPMD\) nội tiếp
Đúng 2
Bình luận (0)
cho tam giác ABC nội tiếp đường tròn tâm (o), đường kính AB2R trên cạnh BC lấy điểm M ( M khác B và C) đường thẳng AM cắt đường tròn O tại D, đường thẳng BD cắt AC tại E đường tròn tâm I ngoại tiếp tam giác MDB cắt đường kính ad tại điểm thứ hai là N1) chứng minh tứ giác CEDM nội tiếp đường tròn và 3 điểm E,M,N thẳng hàng2)cho đoạn thẳng CN cắt đường tròn(i) ở F .cmr : DF//AE
Đọc tiếp
cho tam giác ABC nội tiếp đường tròn tâm (o), đường kính AB=2R trên cạnh BC lấy điểm M ( M khác B và C) đường thẳng AM cắt đường tròn O tại D, đường thẳng BD cắt AC tại E đường tròn tâm I ngoại tiếp tam giác MDB cắt đường kính ad tại điểm thứ hai là N
1) chứng minh tứ giác CEDM nội tiếp đường tròn và 3 điểm E,M,N thẳng hàng
2)cho đoạn thẳng CN cắt đường tròn(i) ở F .cmr : DF//AE
1: góc ACB=góc ADB=1/2*sđ cung AB=90 độ
=>AC vuông góc CB và AD vuông góc DB
=>góc ECM=90 độ=góc EDM
=>CEDM nội tiếp
AC vuông góc CB
AD vuông góc DB
=>AD,BC là 2 đường cao của ΔAEB
=>M là trực tâm
=>AM vuông góc AB
ΔMDB vuông tại D nên ΔMDB nội tiếp đường tròn đường kính MB
=>BM là đường kính của (I)
=>góc MNB=90 độ
=>MN vuông góc AB
=>E,M,N thẳng hàng
b: AM vuông góc AB
=>góc ANM=90 độ
góc ANM+góc ACM=180 độ
=>ACMN nội tiếp
=>góc CAM=góc CNM=góc ADF
=>góc CAM=góc ADF
=>DF//AB
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Hai đường cao BD, CE của tam giác ABC cắt nhau tại H. a) Chứng minh tứ giác BFEC nội tiếp được một đường tròn. b) Kẻ đường kính AD của đường tròn (O). Tứ giác BFCD là hình gì? Vì sao? c) Gọi M là trung điểm của BC. Chứng minh AH = 2OM. d) Chứng minh OA | EF
a) \(BE,CF\) là đường cao của \(\Delta ABC\Rightarrow\hat{BFC}=\hat{BEC}=90^o\).
Mà trong tứ giác \(BFEC\), hai góc này có đỉnh kề nhau và cùng nhìn cạnh \(BC\).
Vậy : Tứ giác \(BFEC\) nội tiếp được một đường tròn (dấu hiệu nhận biết) (đpcm).
b) Ta có : \(\hat{ABD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AB\perp BD.\)
Mà : \(\hat{BFC}=90^o\left(cmt\right)\Rightarrow AB\perp CF.\)
Từ đó suy ra : \(BD\left|\right|CF\Rightarrow BFCD\) là hình thang.
Mà : \(\hat{BFC}=\hat{ABD}=90^o\left(cmt\right)\Rightarrow BFCD\) là hình thang vuông.
c) Ta có : \(CF\left|\right|BD\left(cmt\right)\) hay \(CH\left|\right|BD\left(1\right).\)
Mặt khác : \(\hat{ACD}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AC\perp CD\).
Và : \(BE\perp AC\left(gt\right)\)
Suy ra được : \(CD\left|\right|BE\) hay \(CD\left|\right|BH\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BHCD\) là hình bình hành.
Ta cũng có : \(M\) là trung điểm của \(BC\left(gt\right)\Rightarrow M\) cũng là trung điểm của \(HD\left(3\right).\)
Lại có \(O\) là trung điểm của \(AD\left(4\right)\) (tâm đường tròn).
Từ \(\left(3\right),\left(4\right)\Rightarrow OM\) là đường trung bình của \(\Delta HAD\Rightarrow OM=\dfrac{1}{2}AH\Leftrightarrow AH=2.OM\) (đpcm).
d) Cho \(I\) là giao điểm của \(OA\) và \(EF\).
Ta có : \(\hat{ACB}=\hat{ADB}\) (hai góc nội tiếp cùng chắn \(\stackrel\frown{AB}\)).
Hay : \(\hat{ACB}=\hat{BDI}\left(5\right).\)
Mặt khác : Tứ giác \(BFEC\) nội tiếp được một đường tròn (cmt) nên \(\hat{AFI}=\hat{ECB}\) (cùng bù với \(\hat{BFE}\)) hay \(\hat{AFI}=\hat{ACB}\left(6\right).\)
Từ \(\left(5\right),\left(6\right)\Rightarrow\hat{AFI}=\hat{BDI}\) hay \(\hat{AFI}=\hat{ADB}.\)
\(\Delta ABD:\hat{BAD}+\hat{ADB}=90^o\) (hai góc phụ nhau)
\(\Rightarrow\hat{FAI}+\hat{AFI}=90^o.\)
\(\Delta AFI:\hat{FAI}+\hat{AFI}+\hat{AIF}=180^o\) (tổng ba góc trong một tam giác)
\(\Leftrightarrow\hat{AIF}=180^o-\left(\hat{FAI}+\hat{AFI}\right)=180^o-90^o=90^o\)
\(\Rightarrow OA\perp EF\) (đpcm).
Đúng 1
Bình luận (0)
Cho tam giác ABC (AB<AC) có 3 góc nhọn nội tiếp đường tròn O bán kính R. Ba đường cao AD,BE,CF cắt nhau tại H. Gọi I là tâm đường tròn nội tiếp tam giác ABC, J là tâm đường tròn bàng tiếp góc A. Chứng minh: AI.AJ=AB.AC
Cho tam giác ABC (AB <AC) có 3 góc nhọn nội tiếp trong đường tròn (O; R). Vẽ đường
cao AH của tam giác ABC, đường kính AD của đường tròn. Gọi E, F lần lượt là chân đường vuông
góc kẻ từ C và B xuông đường thẳng AD. M là trung điểm của BC.
a) Chứng minh tứ giác BMOF nội tiếp.
b) Gọi K là giao điểm của AD và BC. Chứng minh KH.ED = KE.BH
a)
Xét (O) có
M là trung điểm của dây BC(gt)
nên OM\(\perp\)BC(Định lí đường kính vuông góc với dây)
Xét tứ giác BMOF có
\(\widehat{BFO}+\widehat{BMO}=180^0\left(90^0+90^0=180^0\right)\)
nên BMOF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 3
Bình luận (0)
cho tam giác ABC có 3 góc nhọn (AB<AC) nội tiếp đường tròn tâm O, gọi AD là đường kính của đường tròn(O). tiếp tuyến tại D của đường tròn (O) cắt BC tại M đường thẳng MO cắt AB và AC lần lượt tại E và F a, CM MD^2 = MC.MB
xét ΔMDC và ΔMBD có
∠M chung
∠MBD=∠MDC=\(\dfrac{1}{2}sđ\stackrel\frown{DC}\)
⇒ΔΔMDC ∼ ΔMBD (g.g)
⇒\(\dfrac{MD}{MB}=\dfrac{MC}{MD}\)⇒MD2=MC.MB
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn( AB AC) nội tiếp đường tròn(0;R) . Các đường cao AD , BE của tam giác ABC cắt nhau tại H .Vẽ đường kính AF của đường tròn ( O) .Gọi M là giao điểm của AD và đường tròn (O) (M khác A )
a )chứng minh rằng tứ giác BHCF là hình bình hành
b ) Chứng minh rằng BC là đường trung trực của đoạn thẳng HM
c) tứ giác BCFM m là hình gì? vì sao?
d) Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng H,G,O thẳng hàng và HG 2GO
Đọc tiếp
Cho tam giác ABC nhọn( AB < AC) nội tiếp đường tròn(0;R) . Các đường cao AD , BE của tam giác ABC cắt nhau tại H .Vẽ đường kính AF của đường tròn ( O) .Gọi M là giao điểm của AD và đường tròn (O) (M khác A ) a )chứng minh rằng tứ giác BHCF là hình bình hành b ) Chứng minh rằng BC là đường trung trực của đoạn thẳng HM c) tứ giác BCFM m là hình gì? vì sao? d) Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng H,G,O thẳng hàng và HG =2GO