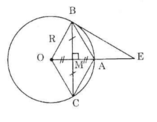
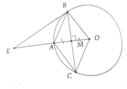
Cho đường tròn (O) có bán kính OA , dây BC vuông góc với OA tại trung điểm M của OA . Tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại E , Tiếp tuyến của đường tròn (O) tại E cắt BE , CE theo thứ tự tại P và Q.
1/ Chứng minh tứ giác OCAB là hình thoi
2/ Biết chu vi tam giác EPQ bằng 2\(\sqrt{3}\) cm
a/ Tính độ dài BE
b/Tính bán kính đường tròn (O)