Đáp án:

 hoặc  

+) Xét 

⇔−15m+53=9⇔−15m+53=9

x1=3m+13; x2=−1x1=3m+13; x2=−1

Theo giả thiết:

\(x^4+2x^3+5x^2+4x-1-m=0\)

\(\Leftrightarrow\left(x^2+x\right)^2+4\left(x^2+x\right)-1-m=0\left(1\right)\)

\(đặt:x^2+x=t\ge\dfrac{-\Delta}{4a}=-\dfrac{1}{4}\)

\(\left(1\right)\Leftrightarrow t^2+4t-1-m=0\) có nghiệm trên \([-\dfrac{1}{4};\text{+∞})\)

\(f\left(t\right)=t^2+4t-1=m\)

\(f\left(-\dfrac{b}{2a}\right)=-5\)

\(f\left(-\dfrac{1}{4}\right)=-\dfrac{31}{16}\Rightarrow m\ge-\dfrac{31}{16}\Rightarrow\left[{}\begin{matrix}t=\dfrac{-b}{2a}=-2\Rightarrow x^2+x+2=0\left(vô-nghiệm\right)\left(loại\right)\\\left\{{}\begin{matrix}t1=\dfrac{-4+\sqrt{20+4m}}{2}=-2+\sqrt{5+m}\\t2=\dfrac{-4-\sqrt{20+4m}}{2}=-2-\sqrt{5+m}\end{matrix}\right.\end{matrix}\right.\) 

\(x^2+x=t1=-2+\sqrt{5+m}\Leftrightarrow f\left(x\right)=x^2+x+2=\sqrt{5+m}\) có nghiệm thuộc \(\left[-1;1\right]\)

\(\Rightarrow f\left(-\dfrac{b}{2a}\right)=\dfrac{7}{4}\)

\(f\left(-1\right)=2;f\left(1\right)=4\)

\(\Rightarrow\dfrac{7}{4}\le\sqrt{5+m}\le4\Leftrightarrow\dfrac{-31}{16}\le m\le11\)

\(x^2+x=t2=-2-\sqrt{5+m}\Leftrightarrow f\left(x\right)=x^2+x+2=-\sqrt{5+m}\)

có nghiệm trên \(\left[-1;1\right]\)

\(x^2+x+2>0\Rightarrow x^2+x+2=-\sqrt{5+m}< 0\left(vô-lí\right)\Rightarrow vô-nghiệm\forall m\)

\(\Rightarrow\dfrac{-31}{16}\le m\le11\) thì pt có  nghiệm thuộc \(\left[-1;1\right]\)

Chọn C.

Đáp án C

Phương pháp:

Đặt 2 x = t t > 0 , đưa về phương trình bậc 2 ẩn t, tìm điều kiện của phương trình bậc 2 ẩn t để phương trình ban đầu có 2 nghiệm phân biệt.

Cách giải: Đặt 2 x = t t > 0 khi đó phương trình trở thành  t 2 − 2 m t + m + 2 = 0 *

Để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt.

Khi  đó:  Δ ' > 0 S > 0 P > 0 ⇔ m 2 − m − 2 > 0 2 m > 0 m + 2 > 0 ⇔ m > 2 m < − 1 m > 0 m > − 2 ⇒ m > 2

Chú ý và sai lầm: Rất nhiều học sinh sau khi đặt ẩn phụ thì quên mất điều kiện t > 0, dẫn đến việc chỉ đi tìm điều kiện đề phương trình (*) có 2 nghiệm phân biệt.

a: \(\text{Δ}=\left(-4\right)^2-4\cdot2\cdot5\left(m-1\right)\)

\(=16-40\left(m-1\right)\)

\(=16-40m+40\)

=-40m+56

Để phương trình có hai nghiệm phân biệt nhỏ hơn 3 thì

\(\left\{{}\begin{matrix}-40m+56>0\\\dfrac{4}{2}< 6\end{matrix}\right.\Leftrightarrow-40m>-56\)

hay m<7/5

b: Để phương trình có hai nghiệm phân biệt lớn hơn 3 thì

\(\left\{{}\begin{matrix}-40m+56>0\\\dfrac{4}{2}>6\end{matrix}\right.\Leftrightarrow m\in\varnothing\)

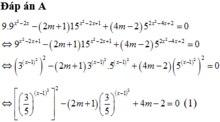
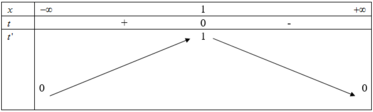
Dựa vào bảng biến thiên hàm f(x), ta thấy để phương trình (1) có 2 nghiệm thực x phân biệt thì phương trình (2) phải có duy nhất 1 nghiệm thuộc khoảng (0;1), nghiệm còn lại (nếu có) khác 1. Số nghiệm của (2) là số giao điểm của đồ thị hàm số y = 3 5 x - 1 2  và đường thẳng y = 2 m - 1  nên điều kiện của m thỏa mãn là  0 < 2 m - 1 < 1 ⇔ 1 2 < m < 1