a)\(\frac{{15}}{8} = 1,875;\,\,\,\,\,\,\,\frac{{ - 99}}{{20}} =  - 4,95;\,\,\,\,\,\,\\\frac{{40}}{9} = 4,\left( 4 \right);\,\,\, - \frac{{44}}{7} =  - 6,(285714)\)

b) Trong các số thập phân trên, số thập phân 4,(4) và -6,(285714) là các số thập phân vô hạn tuần hoàn với chu kì lần lượt là 4 và 285714

- Ta có:

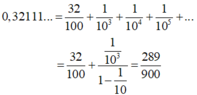
- Vậy a = 289, b = 900.

- Do đó: a - b = 289 – 900 = - 611.

Chọn B.

Đáp án C

Ta có:

0 , 32111 . . . = 32 100 + 1 10 3 + 1 10 4 + 1 10 5 + . . . = 32 100 + 1 10 3 1 - 1 10 = 289 900  .

Vậy a = 289 , b = 900 . Do đó a - b = 289 - 900 = - 611 .

a: Các số biểu diễn dưới dạng thập phân hữu hạn là 

\(3\dfrac{1}{4}=3,25\)

\(\dfrac{7}{32}=0.21875\)

\(\frac{{12}}{{25}} = 0,48;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{27}}{2} = 13,5;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{10}}{9} = 1,(1)\)

\(\dfrac{12}{25}=\dfrac{12\times4}{25\times4}=\dfrac{48}{100}=0,48\)

\(\dfrac{27}{2}=\dfrac{27\times5}{2\times5}=\dfrac{135}{10}=13,5\)

\(\dfrac{10}{9}=1+\dfrac{1}{9}=1+0,\left(1\right)=1,\left(1\right)=1,111...\)

Chọn B,C

Câu 1: 

\(\dfrac{24}{10}=2.4\)

\(\dfrac{225}{100}=2.25\)

\(\dfrac{6453}{1000}=6.453\)

\(\dfrac{25789}{10000}=2.5789\)