Cho tam giác MNP cân tại P có PM = PN = 15 cm, MN = 18cm. Kẻ PI ⊥ MN (I ϵ MN). Kẻ IH ⊥ MP (H ϵ MP), IK ⊥ NP (K ϵ NP)
a) Chứng minh rằng ΔMIP = ΔNIP
b) Chứng minh rằng IH = IK
c) Tính độ dài IP
d) Chứng minh HK // AB
Cho tam giác MNP cân tại P có PM = PN = 15 cm, MN = 18cm. Kẻ PI ⊥ MN (I ϵ MN). Kẻ IH ⊥ MP (H ϵ MP), IK ⊥ NP (K ϵ NP)
a) Chứng minh rằng ΔMIP = ΔNIP
b) Chứng minh rằng IH = IK
c) Tính độ dài IP
d) Chứng minh HK // AB
Cho tam giác MNP cân tại M có MN =MP 8cm , NP=10cm.
Kẻ MI vuông góc với NP (I thuộc NP)
a chứng minh rằng: IB =IC
b. Kẻ IH vuông góc với MN (H thuộc MN),IK vuông với MP (K thuộc MP). Chứng minh IH=IK
cho tam giác MNP cân tại M coa MN=MP=13cm, NP=10cm. kẻ MI vuông góc với NP (IϵNP)
A, chứng minh rằng: IN=IP
B,tính độ dài MI
C, kẻ IH vuông góc với MN (HϵMN), IK vuông góc với MP (KϵMP).chứng minh IH=IK
Xét tam giác MNI và MPI có
MI là cạnh chung
MN = MP( tam giác MNP cân)
Góc MIN = góc MIP = 90°
=> Tam giác MIN = tam giác MIP( cgv - ch)
IN = IP = 5 cm nên I là trung điểm của NP
b) Tam giác MIN vuông tại I có
NI2 + MI2 = MN2( định lí Pytago)
MI2 + 52 = 142
MI2 + 25 = 196
MI2 = 144
MI=12
c) Xét tam giác PHI và PKI có
MI là cạnh chung
Góc HMI = KMI ( tam giác NMI = PMI )
Góc IHM = IKM = 90°
=》 Tam giác HMI = KMI ( ch - gn)
=》IH=IK
Cho tam giác MNP có MP = 20cm, I là trung điểm của MN, K là trung điểm của MP.
a) Chứng minh IK là đường trung bình của tam giác MNP.
b) Qua K kẻ KH // MN ( H thuộc NP). Chứng minh H là trung điểm của NP.
c) Chứng minh IH // MP, tính độ dài của đoạn thẳng IH.
giúp em nhanh với ạ em đang cần gấp ạ
\(a,\left\{{}\begin{matrix}MI=IN\\MK=KP\end{matrix}\right.\Rightarrow IK\) là đường trung bình tam giác MNP
\(b,\left\{{}\begin{matrix}MK=KP\\HK//MN\end{matrix}\right.\Rightarrow NH=HP\) hay \(H\) là trung điểm NP
\(c,\left\{{}\begin{matrix}MI=IN\\NH=HP\end{matrix}\right.\Rightarrow IH\) là đường trung bình tam giác MNP
\(\Rightarrow IH=\dfrac{1}{2}MP=10\left(cm\right)\)
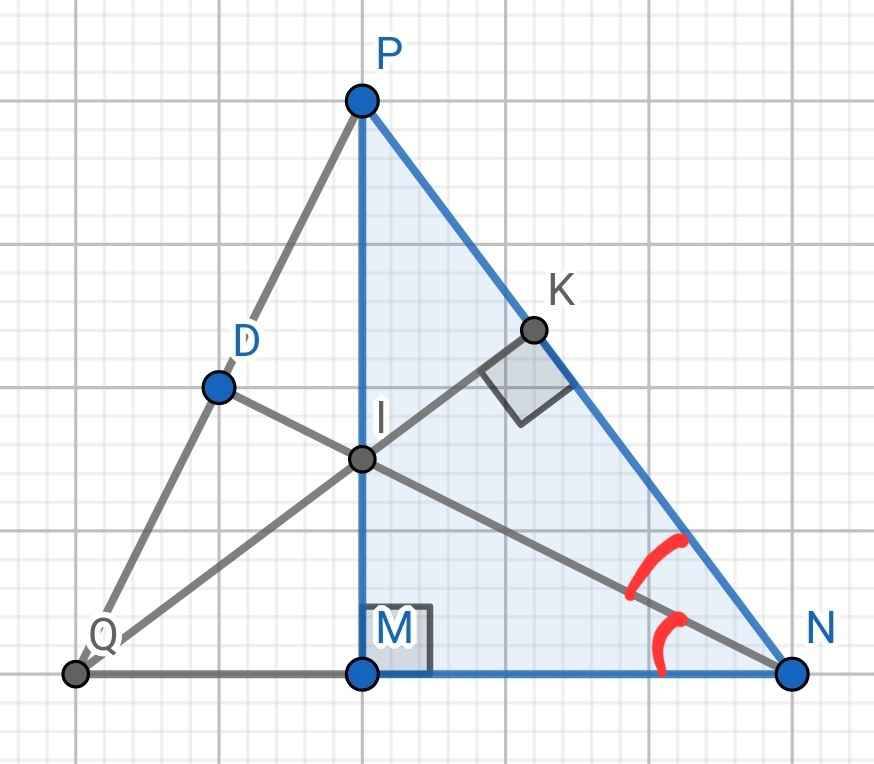
Cho ∆MNP vuông tại M có MN< MP. Kẻ đường phân giác NI của góc MNP ( I thuộc MP) .kẻ IK vuông góc NP a. Chứng minh rằng ∆IMN=∆IKN b. chứng minh rằng MI < IP c. Gọi Q là giao điểm của IK và MN , đường thẳng NI cắt QP tại D. Chứng minh rằng ND vuông góc QP
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
Cho tam giác MNP cân ở P , MN=6 , PI là phân giác của góc P ( I thuộc MN )
a) Chứng minh : Tam giác MPI = tam giác NPI
b) Kẻ IK vuông góc với PM tại K , IH vuông góc với PN tại H .
Chứng minh : IP là phân giác của góc KIH
c) Trên tia đối của tia IP , lấy điểm Q sao cho IQ = IM . Chứng minh rằng : Tam giác MIQ vuông cân . Từ đó , tính độ dài đoạn MQ .
d) Tam giác MNP cần thêm điều kiện gì để tam giác IKH đều .
Bài 4:Cho tam giác ABC có CA = CB = 10cm, AB = 12cm. Kẻ CI \(\perp\) AB (I ϵ AB). Kẻ IH \(\perp\) AC (H ϵ AC), IK \(\perp\) BC (K ϵ BC)
a, Chứng minh rằng IA = IB
b, Chứng minh rằng IH = IK
c, Tính độ dài IC
d, HK // AB
a: Xét ΔCIA vuông tại I và ΔCIB vuông tại I có
CA=CB
CI chung
Do đó: ΔCIA=ΔCIB
Suy ra: IA=IB
b: Xét ΔCHI vuông tại H và ΔCKI vuông tại K có
CI chung
\(\widehat{HCI}=\widehat{KCI}\)
Do đó: ΔCHI=ΔCKI
Suy ra: IH=IK
c: IA=IB=AB/2=6(cm)
nen IC=8(cm)
d: Xét ΔCAB có CH/CA=CK/CB
nên HK//AB
Cho tam giác MNP cân ở P, MN = 6 cm, PI là phân giác của góc MPN (I thuộc MN)
a, Chứng minh: Tam giác MPI = Tam giác NPI
b, Kẻ IK vuông góc với PM tại K, IH vuông góc với PN tại H.
Chứng minh: IP là phân giác của góc KIH
c, Trên tia đối của tia IP, lấy điểm Q sao cho IQ = IM
Chứng minh: Tam giác MIQ vuông cân. Tính độ dài MQ.
d, Tam giác MNP cần thêm điều kiện gì để tam giác PKH đều?
| GT | △MNP cân tại P. MN = 6cm, NPI = MPI = NPM/2 , (I IK ⊥ PM , IH ⊥ PN . IQ = IM |
KL | a, △MPI = △NPI b, HIP = PIK c, △MIQ vuông cân. MQ = ? d, Nếu PKH đều, điều kiện △MNP |
Bài làm:
a, Vì △MNP cân tại P => PN = PM
Xét △NPI và △MPI
Có: NP = MP (gt)
NPI = MPI (gt)
PI là cạnh chung
=> △NPI = △MPI (c.g.c)
b, Xét △HPI vuông tại H và △KPI vuông tại K
Có: PI là cạnh chung
HPI = KPI (gt)
=> △HPI = △KPI (ch-gn)
=> HIP = PIK (2 góc tương ứng)
Mà IP nằm giữa IH, IK
=> IP là phân giác KIH
c, Ta có: PIN = MIQ (2 góc đối đỉnh)
Mà PIN = 90o (gt)
=> MIQ = 90o (1)
Xét △MIQ có: IQ = IM => △MIQ cân tại I (2)
Từ (1), (2) => △MIQ vuông cân tại I
Vì △NPI = △MPI (cmt)
=> IN = IM (2 cạnh tương ứng)
Mà MN = IN + IM = 6 (cm)
=> IN = IM = 6 : 2 = 3 (cm)
Mà IM = IQ
=> IM = IQ = 3 (cm)
Xét △MIQ vuông tại I có: IQ2 + IM2 = MQ2 (định lý Pitago)
=> 32 + 32 = MQ2
=> 9 + 9 = MQ2
=> 18 = MQ2
=> MQ = \(\sqrt{18}=3\sqrt{2}\)
d, Để △PHK đều <=> HPK = PKH = KHP = 60o
=> △MNP có NPM = 60o mà △MNP cân
=> △MNP đều
Vậy để △PKH đều <=> △MNP đều
cho tam giác MNP vuông tại M có MN= 3cm, gọi I là trung điểm của MP, K là trung điểm của NP
a, chứng minh IK//MN
b, tính IK
c, gọi H là trung điểm của MN, tứ giác IKNH là hình gì? vì sao?
d,tính độ dài đường chéo IH biết IP= 2cm