Các câu hỏi tương tự
cho tam giác MNP cân tại M coa MN=MP=13cm, NP=10cm. kẻ MI vuông góc với NP (IϵNP)
A, chứng minh rằng: IN=IP
B,tính độ dài MI
C, kẻ IH vuông góc với MN (HϵMN), IK vuông góc với MP (KϵMP).chứng minh IH=IK
Cho tam giác MNP can tại M, kẻ đường cao MI.
a, Chứng minh tam giác MIN= tam giác MIP
b, Kẻ IH vuông góc Mp, Ik vuông góc MN (H thuộc Mp, K thuộc MN). Chứng minh NH=NK
c, So sánh KH và NP
Cho tam giác MNP cân tại A có MN = MP = 5 cm ; NP= 8cm
Kẻ MH vuông góc với NP (H thuộc NP).
a. Chứng minh HN = HP và
b. Tính độ dài MH
c. Kẻ HD vuông góc MN (D thuộc MN) Kẻ HE vuông góc MP (E thuộc MP).Chứng minh DHDE là tam giác cân.
Cho tam giác MNP cân tại Mc.Kẻ Nk vuông góc với MP ( k thuộc MP ).Kẻ PH vuông góc với MN ( h thuộc MN ).NK và PH cắt nhau tại I.
a.chứng minh rằng tam giác HNP=tam giác KPN.
b.so sánh góc HNI và góc KPI.
c.Đường thẳng MI cắt NP tại D,chứng minh rằng MD vuông góc với NP tại D
d.chứng minh rằng HK//NP
Cho ∆MNP vuông tại M, MN < MP phân giác NI, I thuộc MP gọi H là hình chiếu của I trên Np lấy B thuộc MP sao cho MB=MN từ B kẻ đường thẳng d vuông góc với MP và cắt tia IH tại K. Chứng minh góc INK= 45°
Cho ∆MNP vuông tại M, MN < MP phân giác NI, I thuộc MP gọi H là hình chiếu của I trên Np lấy B thuộc MP sao cho MB=MN từ B kẻ đường thẳng d vuông góc với MP và cắt tia IH tại K. Chứng minh góc INK= 45°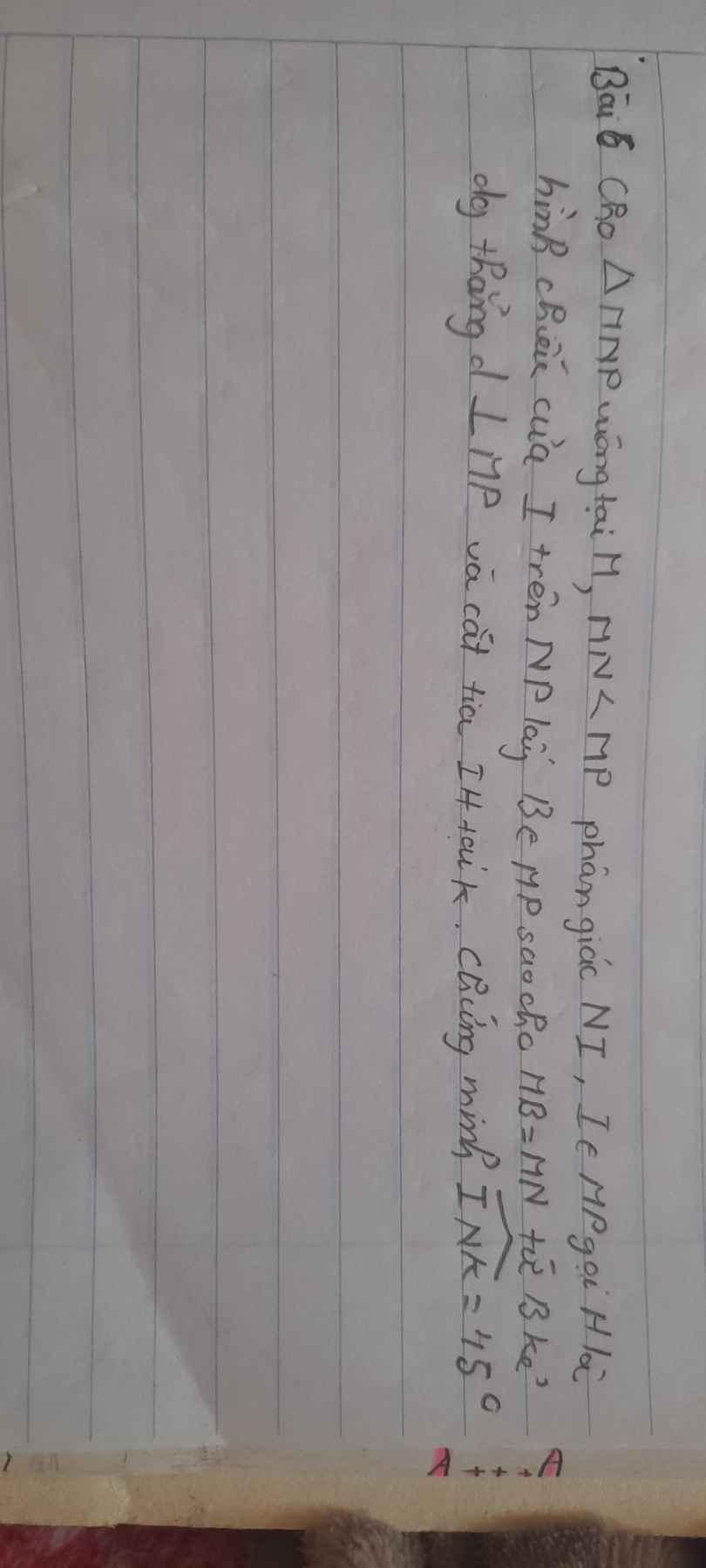
Cho ∆MNP vuông tại M, MN < MP phân giác NI, I thuộc MP gọi H là hình chiếu của I trên Np lấy B thuộc MP sao cho MB=MN từ B kẻ đường thẳng d vuông góc với MP và cắt tia IH tại K. Chứng minh góc INK= 45°
cho tam giác MNP cân tại M kẻ MH vuông góc với NP(H thuộc NP)a) chứng minh HN=HPb)kẻ HI vuông góc với MN (I thuộc MN ),HE vuông góc với MP (E thuộc MP)chứng minh tam giá HIE cânc)nếu cho góc NMP=120 độ thì tam giác HIE trở thành tam giác gì?vì sao?cá...
Câu 11. Cho MNP vuông tại M có MN MP, kẻ đường phân giác NI của góc MNP (I thuộc MP ). Kẻ IK vuông góc với NP tại K .a) Chứng minh IMN IKNb) Gọi A là giao của NM và KT. Chứng minh AMI PKI và KI AIc) Từ P kẻ đường thẳng vuông góc với NI tại H . Chứng minh A; H; P thẳng hàng
Đọc tiếp
Câu 11. Cho ![]() MNP vuông tại M có MN < MP, kẻ đường phân giác NI của góc MNP (I thuộc MP ). Kẻ IK vuông góc với NP tại K .
MNP vuông tại M có MN < MP, kẻ đường phân giác NI của góc MNP (I thuộc MP ). Kẻ IK vuông góc với NP tại K .
a) Chứng minh ![]() IMN =
IMN = ![]() IKN
IKN
b) Gọi A là giao của NM và KT. Chứng minh ![]() AMI =
AMI = ![]() PKI và KI < AI
PKI và KI < AI
c) Từ P kẻ đường thẳng vuông góc với NI tại H . Chứng minh A; H; P thẳng hàng








