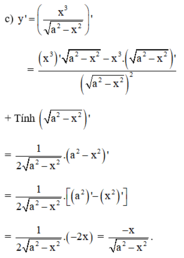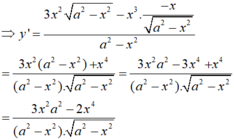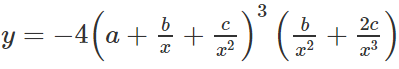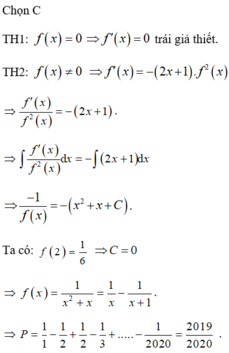Tính đạo hàm của C/ f2 (x) (C là hằng số

Những câu hỏi liên quan
Tính đạo hàm của các hàm số sau:
a) \(y = {x^2} + 1;\)
b) \(y = kx + c\) (với k, c là các hằng số).
a: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{x^2+1-x_0^2-1}{x-x_0}\)
\(=\lim\limits_{x\rightarrow x0}\dfrac{\left(x-x0\right)\left(x+x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}x+x0=x0+x0=2x0\)
b: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}\)
\(=\lim\limits_{x\rightarrow x0}\dfrac{kx+c-k\cdot x0-c}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{k\left(x-x0\right)}{x-x0}\)
=\(\lim\limits_{x\rightarrow x0}k=k\)
Đúng 1
Bình luận (0)
Sử dụng định nghĩa, tìm đạo hàm của các hàm số sau:
a) \(y = k{x^2} + c\) (với k, c là các hằng số);
b) \(y = {x^3}.\)
a) Với \({x_0}\) bất kì, ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k{x^2} + c - \left( {kx_0^2 + c} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k\left( {{x^2} - x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{k\left( {x - {x_0}} \right)\left( {x + {x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left[ {k\left( {x + {x_0}} \right)} \right] = 2k{x_0}\)
Vậy hàm số \(y = k{x^2} + c\) có đạo hàm là hàm số \(y' = 2kx\)
b) Với \({x_0}\) bất kì, ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2\)
Vậy hàm số \(y = {x^3}\) có đạo hàm là hàm số \(y' = 3{x^2}\)
Đúng 0
Bình luận (0)
Chứng minh khẳng định trong nhận xét trên.
a) Đạo hàm của hàm hằng bằng 0: c ’ = 0 .
b) Đạo hàm của hàm số y = x bằng 1: x ’ = 1 .
a) Hàm hằng ⇒ Δy = 0
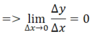
b) theo định lí 1
y = x hay y = x1 ⇒ y’= (x1)’= 1. x1-1 = 1. xo = 1.1 =1
Đúng 0
Bình luận (0)
Tính đạo hàm \(f'\left( {{x_0}} \right)\) tại điểm \({x_0}\) bất kì trong các trường hợp sau:
a) \(f\left( x \right) = c\) (c là hằng số);
b) \(f\left( x \right) = x.\)
a: \(f'\left(x_0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{c-c}{x-x0}=0\)
b: \(f'\left(x0\right)=\lim\limits_{x\rightarrow x0}\dfrac{f\left(x\right)-f\left(x0\right)}{x-x0}=\lim\limits_{x\rightarrow x0}\dfrac{x-x0}{x-x0}=1\)
Đúng 0
Bình luận (0)
Tính đạo hàm của các hàm số sau: y = x 3 a 2 - x 2 a là hằng số
Tìm đạo hàm của hàm số sau :
\(y=\left(a+\dfrac{b}{x}+\dfrac{c}{x^2}\right)^4\) (a, b, c là các hằng số)
Cho hàm số y f(x) có đạo hàm liên tục trên khoảng
0
;
+
∞
, biết
f
x
+
2
x
+
1
f
2
x
0
,
∀
x
0
và
f
2...
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm liên tục trên khoảng 0 ; + ∞ , biết f ' x + 2 x + 1 f 2 x = 0 , ∀ x > 0 và f 2 = 1 / 6 . Tính giá trị của biểu thức P = f 1 + f 2 + . . . + f 2019 .
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Đạo hàm của hàm số
f
(
x
)
a
3
-
3
a
t
2
-
5
t
3
(với a là hằng số) bằng biểu thức nào sau đây? A.
3
a
2
-
6
a
t
-
15
t
2
B.
3
a
2
-
3...
Đọc tiếp
Đạo hàm của hàm số f ( x ) = a 3 - 3 a t 2 - 5 t 3 (với a là hằng số) bằng biểu thức nào sau đây?
A. 3 a 2 - 6 a t - 15 t 2
B. 3 a 2 - 3 t 2
C. - 6 a t - 15 t 2
D. 3 a 2 - 3 t 2 - 6 a t - 15 t 2
Cho f(x), g(x) là các hàm số có đạo hàm liên tục trên
ℝ
số
k
∈
ℝ
và C là một hằng số tùy ý. Xét 4 mệnh đề sau
I
:
∫
f
x
d
x
f
x
I
I
:
∫
k
f
x
d
x
k
∫...
Đọc tiếp
Cho f(x), g(x) là các hàm số có đạo hàm liên tục trên ℝ số k ∈ ℝ và C là một hằng số tùy ý. Xét 4 mệnh đề sau
I : ∫ f x d x ' = f x
I I : ∫ k f x d x = k ∫ f x d x
I I I : ∫ f x + g x d x = ∫ f x d x + ∫ g x d x
I V : ∫ x 2 d x = x 3 3 + C
Số mệnh đề đúng là
A. 1
B. 2
C. 4
D. 3