Điểm A(0;1;2) và d:\(\left\{{}\begin{matrix}x=1+t\\y=2-2t\\z=1\end{matrix}\right.\). Đường thẳng (△) đi qua A và cắt d tại điểm B sao cho AB = 2. Viết phương trình tham số của đường thẳng △. ( Biết tọa độ của B là các giá trị nguyên)

Những câu hỏi liên quan
Bài 3: Xác định đường thẳng (d):
a) Đi qua 2 điểm A(-3; 0) và B(0; 2)
b) Đi qua 2 điểm A(0; 1) và B(-1; 0)
c) Đi qua 2 điểm A(0; -3) và B(1;- 1)
\(a,\) Gọi pt đường thẳng \(\left(d\right)\) là \(y=ax+b\)
Ta có \(\left(d\right)\) đi qua \(A\left(-3;0\right),B\left(0;2\right)\) nên \(\left\{{}\begin{matrix}0=-3a+b\\2=0a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b=2\end{matrix}\right.\)
Vậy đths là \(\left(d\right):y=\dfrac{2}{3}x+2\)
\(b,\) Gọi pt đường thẳng \(\left(d\right)\) là \(y=ax+b\)
Ta có hệ pt \(\left\{{}\begin{matrix}1=0a+b\\0=-a+b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\)
Vậy đths là \(\left(d\right):y=x+1\)
Đúng 2
Bình luận (0)
a,a, Gọi pt đường thẳng (d)(d) là y=ax+by=ax+b
Ta có (d)(d) đi qua A(−3;0),B(0;2)A(−3;0),B(0;2) nên {0=−3a+b2=0a+b⇔⎧⎨⎩a=23b=2{0=−3a+b2=0a+b⇔{a=23b=2
Vậy đths là (d):y=23x+2(d):y=23x+2
b,b, Gọi pt đường thẳng (d)(d) là y=ax+by=ax+b
Ta có hệ pt {
Đúng 2
Bình luận (0)
Từ điểm A nằm ngoài đường tròn (0;R). Vẽ 2 tiếp tuyến AB,AC của đường tròn (0) (A,B là các tiếp điểm) Vẽ đường kính BD của đường tròn (0) AD cắt đường tròn (0) tại điểm thứ 2 là E, gọi K là trung điểm DE. a) C/m: 5 điểm A,B,0,K,C cùng thuộc 1 đường tròn (0) b) C/m: AD.AE=AC^2
Cho các điểm A(-1; 0), B(0; 2), C(2; -3), D(3; 0), O(0; 0). Có bao nhiêu điểm nằm trên trục hoành trong số các điểm trên?
A. 0
B. 1
C. 2
D. 3
Các điểm nằm trên trục hoành là các điểm có tung độ bằng 0. Trong số các điểm ở trên ta thấy những điểm có tung độ bằng 0 là: A(-1; 0), D(3; 0), O(0; 0) . Vậy có ba điểm nằm trên trục hoành
Chọn đáp án D
Đúng 0
Bình luận (0)
Câu 1. [VDT] Biết đường thẳng y = ax + b cắt trục hoành tại điểm có hoành độ âm và cắt trục tung tại điểm có tung độ dương. Khẳng định nào sau đây đúng?
A. a < 0 và b > 0. B. a < 0 và b < 0.
C. a > 0 và b < 0. D. a > 0 và b > 0.
Trong không gian Oxyz, cho hai điểm A(2; 0; 0), B(0; 0; 8) và điểm C sao cho AC → = (0; 6; 0). Tính khoảng cách từ trung điểm I của BC đến đường thẳng OA.

Do đó I(1; 3; 4)
Phương trình mặt phẳng ( α ) qua I và vuông góc với OA là: x – 1 = 0, ( α ) cắt OA tại K(1; 0; 0)
Khoảng cách từ I đến OA là:
![]()
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy cho ba điểm A(a; 0); B(0; b) (với a 0, b 0) và C(1; 2) như trên hình 12.a) Viết phương trình đường thẳng đi qua hai điểm A, B.b) Tìm hệ thức liên hệ giữa a, b sao cho ba điểm A, B, C thẳng hàng.c) Tìm các giá trị của a, b sai cho bao điểm A, B, C thẳng hàng và diện tích tam giác OAB nhỏ nhất.
Đọc tiếp
Trên mặt phẳng tọa độ Oxy cho ba điểm A(a; 0); B(0; b) (với a > 0, b > 0) và C(1; 2) như trên hình 12.
a) Viết phương trình đường thẳng đi qua hai điểm A, B.
b) Tìm hệ thức liên hệ giữa a, b sao cho ba điểm A, B, C thẳng hàng.
c) Tìm các giá trị của a, b sai cho bao điểm A, B, C thẳng hàng và diện tích tam giác OAB nhỏ nhất.

a,Vẽ một trục số và cho biết những điểm nào cách điểm 0 là 2 đơn vị.
b,Trên trục số hãy ghi điểm A cách điểm 0 là 3 đơn vị về phía bên trái, điểm B cách điểm gốc 0 là 2 đơn vị về phía bên phải.
Câu 9. Cho bản đồ sau:Tìm điểm có tọa độ (0°, 130°Đ)?A. Điểm G. B. Điểm H. C. Điểm C. D. Điểm E.Câu 10. Điểm E trên hình 12 có tọa độ địa lí bao nhiêu?A. (0°, 140°Đ) B. (0°, 125°Đ) C. (10°B, 130°Đ) D. (15°B, 130°Đ)Câu 11. Trên hình 12, máy bay đi từ Hà Nội đến Băng Cốc (Thái Lan), bay theo hướng nào sau đây ?A. Hướng Nam B. Hướng Tây C. Hướng Bắc D. Hướng Tây NamCâu 12. Cho bản đồ hướng di chuyển của cơn bão...
Đọc tiếp
Câu 9. Cho bản đồ sau: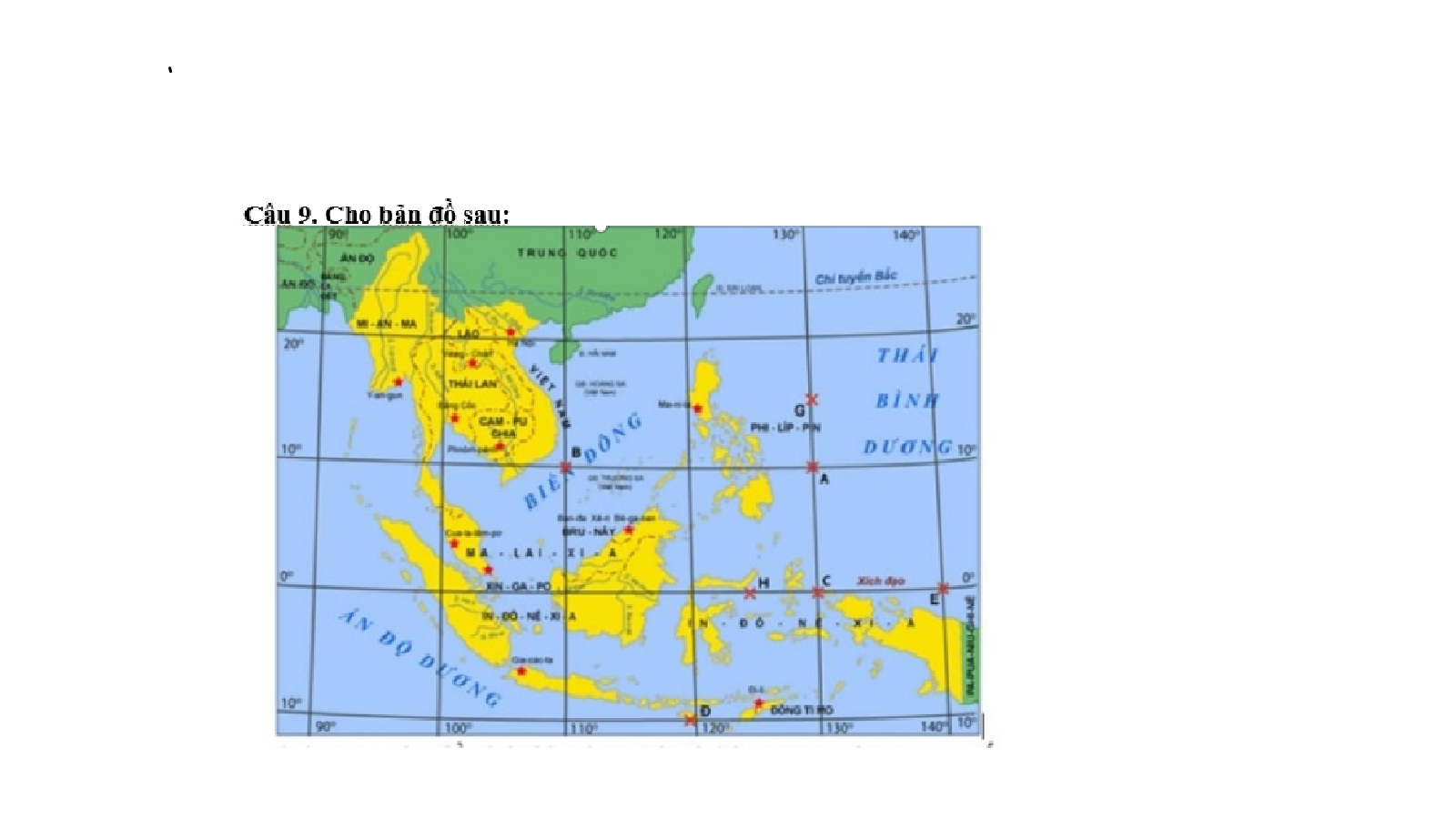
Tìm điểm có tọa độ (0°, 130°Đ)?
A. Điểm G. B. Điểm H. C. Điểm C. D. Điểm E.
Câu 10. Điểm E trên hình 12 có tọa độ địa lí bao nhiêu?
A. (0°, 140°Đ) B. (0°, 125°Đ) C. (10°B, 130°Đ) D. (15°B, 130°Đ)
Câu 11. Trên hình 12, máy bay đi từ Hà Nội đến Băng Cốc (Thái Lan), bay theo hướng nào sau đây ?
A. Hướng Nam B. Hướng Tây C. Hướng Bắc D. Hướng Tây Nam
Câu 12. Cho bản đồ hướng di chuyển của cơn bão Doksuri đổ bộ vào nước ta:
Bão Doksuri di chuyển vào nước ta theo hướng
A. Tây Bắc. B. Đông Nam. C. Tây. D. Bắc.
Câu 13. Khoảng cách từ một điểm đến vĩ tuyến gốc xác định là
A. kinh độ của điểm đó. B. vĩ độ của điểm đó.
C. tọa độ địa lí của điểm đó. D. điểm cực đông của điểm đó
Cho đường thẳng Δ : x – y + 2 = 0 và hai điểm O(0; 0), A(2; 0).
a, Tìm điểm đối xứng của O qua Δ.
b, Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
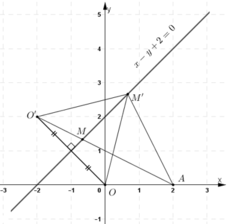
a, Cách 1: Gọi O’ là điểm đối xứng với O qua (Δ)
⇒ OO’ ⊥ Δ tại trung điểm I của OO’.
+ (Δ) nhận 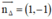 là một vtpt ⇒ (Δ) nhận
là một vtpt ⇒ (Δ) nhận 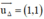 là một vtcp
là một vtcp
OO’ ⊥ Δ ⇒ OO’ nhận 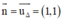 là một vtpt. Mà O(0, 0) ∈ OO’
là một vtpt. Mà O(0, 0) ∈ OO’
⇒ Phương trình đường thẳng OO’: x + y = 0.
+ I là giao OO’ và Δ nên tọa độ của I là nghiệm của hệ phương trình:
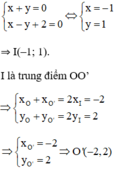
Cách 2: Gọi O’(x, y) là điểm đối xứng với O qua Δ.
+ Trung điểm I của OO’ là 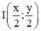
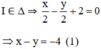
+ (Δ) nhận 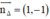 là một vtpt ⇒ (Δ) nhận
là một vtpt ⇒ (Δ) nhận 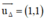 là một vtcp.
là một vtcp.
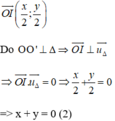
Từ (1) và (2) ta có hệ phương trình
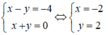
Vậy O’(–2; 2).
b)
+ Vì O và A nằm cùng một nửa mặt phẳng bờ là đường thẳng Δ nên đoạn thẳng OA không cắt Δ.
O’ và A thuộc hai nửa mặt phẳng khác nhau bờ là đường thẳng Δ nên O’A cắt Δ.
Do O’ đối xứng với O qua đường thẳng ∆ nên ∆ là đường trung trực của đoạn thẳng OO’, với mọi M ∈ Δ ta có MO = MO’.
Độ dài đường gấp khúc OMA bằng OM + MA = O’M + MA ≥ O’A.
⇒ O’M + MA ngắn nhất khi O’M + MA = O’A ⇔ M là giao điểm của O’A và Δ.
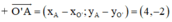
⇒ O’A nhận 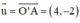 là một vtcp
là một vtcp
⇒ O’A nhận 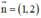 là một vtpt. Mà A(2; 0) ∈ O’A
là một vtpt. Mà A(2; 0) ∈ O’A
⇒ Phương trình đường thẳng O’A : 1(x - 2) + 2(y - 0)= 0 hay x + 2y – 2 = 0.
M là giao điểm của O’A và Δ nên tọa độ điểm M là nghiệm của hệ :
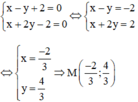
Vậy điểm M cần tìm là 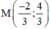
Đúng 0
Bình luận (0)
Trên trục số điểm 1 cách điểm 0 là 1 đơn vị theo chiều dương, điểm –1 cách điểm 0 là 1 đơn vị theo chiều âm.Điền vào chỗ trống trong các câu sau.a) Điểm –3 cách điểm 0 là ..... đơn vị theo chiều .....b) Điểm 3 cách điểm 0 là ..... đơn vị theo chiều .....c) Điểm –5 cách điểm 0 là ..... đơn vị theo chiều .....d) Điểm 4 cách điểm 0 là ..... đơn vị theo chiều .....
Đọc tiếp
Trên trục số điểm 1 cách điểm 0 là 1 đơn vị theo chiều dương, điểm –1 cách điểm 0 là 1 đơn vị theo chiều âm.
Điền vào chỗ trống trong các câu sau.
a) Điểm –3 cách điểm 0 là ..... đơn vị theo chiều .....
b) Điểm 3 cách điểm 0 là ..... đơn vị theo chiều .....
c) Điểm –5 cách điểm 0 là ..... đơn vị theo chiều .....
d) Điểm 4 cách điểm 0 là ..... đơn vị theo chiều .....
a) .....3.....âm.....
b) .....3.....dương.....
c) .....5.....âm.....
d) .....4,,,,,dương.....
Đúng 0
Bình luận (0)
















