Bạn giúp mình tí.
-4m -1 -2m2 -2m > \(\frac{5m+5}{m-2}\)
Những câu hỏi liên quan
16 tháng 9 2021 lúc 22:25
Tìm m để phương trình sau có 5 nghiệm phân biệt thuộc khoảng \(\left(-\dfrac{\pi}{2};3\pi\right)\)
2sin2x - (5m + 1)sinx + 2m2 + 2m = 0
Từ đường tròn lượng giác, trên \(\left(-\dfrac{\pi}{2};3\pi\right)\):
- Nếu \(0< t< 1\) thì \(sinx=t\) có 4 nghiệm
- Nếu \(-1< t< 0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=1\) thì \(sinx=t\) có 2 nghiệm
- Nếu \(t=-1\) thì \(sinx=t\) có 1 nghiệm
Do đó pt đã cho có 5 nghiệm pb trong khoảng đã cho khi:
\(2t^2-\left(5m+1\right)t+2m^2+2m=0\) có 2 nghiệm pb thỏa mãn:
- TH1: \(\left\{{}\begin{matrix}t_1=-1\\0< t_2< 1\end{matrix}\right.\)
- TH2: \(\left\{{}\begin{matrix}-1< 0< t_1\\t_2=1\end{matrix}\right.\)
- TH3: \(\left\{{}\begin{matrix}t_1=0\\t_2=1\end{matrix}\right.\)
Về cơ bản, chỉ cần thay 1 nghiệm bằng 0 hoặc 1 rồi kiểm tra nghiệm còn lại có thỏa hay ko là được
Đúng 1
Bình luận (1)
Cho m là số nguyên.Chứng minh 4m^3+9m^2-19m-30 chia hết cho 6Mình giải được đến đâ rôi sao nữa vậy?4m^3+9m^2-19m-304m^3+4m^2-24m+5m^2+5m^2-30 4m(m^2+m-6)+5(m^2+m-6) (4m+5)(m^2+3m-2m-6) (4m+5)(m^2-2m+3m-6) (4m+5)(m(m-2)+3(m-2)) (4m+5)(m+3)(m-2)
Đọc tiếp
Cho m là số nguyên.Chứng minh 4m^3+9m^2-19m-30 chia hết cho 6
Mình giải được đến đâ rôi sao nữa vậy?
4m^3+9m^2-19m-30=4m^3+4m^2-24m+5m^2+5m^2-30
=4m(m^2+m-6)+5(m^2+m-6)
=(4m+5)(m^2+3m-2m-6)
=(4m+5)(m^2-2m+3m-6)
=(4m+5)(m(m-2)+3(m-2))
=(4m+5)(m+3)(m-2)
Nếu m có dạng 3k thì m+3 chia hết cho 3, nếu m có dạng 3k-1 thì m-2 chia hết cho 3
Đúng 0
Bình luận (0)
Biết rằng
m
m
0
thì phương trình
2
sin
2
x
-
5
m
+
1
sin
x
+
2
m
2
+
2
m
0
có đúng 5 nghiệm phân biệt thuộc
-...
Đọc tiếp
Biết rằng m = m 0 thì phương trình 2 sin 2 x - 5 m + 1 sin x + 2 m 2 + 2 m = 0 có đúng 5 nghiệm phân biệt thuộc - π 2 ; 3 π . Mệnh đề nào sau đây đúng?
Cho hai hàm số
f
x
1
3
x
3
−
m
+
1
x
2
+
3
m
2
+
4
m
+
5
x
+
2019
v...
Đọc tiếp
Cho hai hàm số f x = 1 3 x 3 − m + 1 x 2 + 3 m 2 + 4 m + 5 x + 2019 và g x = m 2 + 2 m + 5 x 3 − 2 m 2 + 4 m + 9 x 2 − 3 x + 2 (với m là tham số). Hỏi phương trình g f x = 0 có bao nhiêu nghiệm?
A. 9
B. 0
C. 3
D. 1
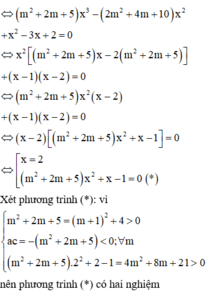
Vì f(x) là hàm đồng biến nên mỗi phương trình (1);(2);(3) đều chỉ có 1 nghiệm duy nhất và ba nghiệm của phương trình này khác nhau.
Từ đó phương trình g f x = 0 có ba nghiệm phân biệt.
Chọn: C
Đúng 0
Bình luận (0)
Người thứ nhất mua 4m vải hoa và 9m vải lụa hết 350000đồng.Người thứ hai mua 2m vải hoa và 5m vải lụa hết 190000 đồng.Tính giá tiền 1m vải hoa và 1m vải lụa.
Các bạn giúp mình với.Ai nhanh mình sẽ tick cho người đó 1 tick
Viết số thích hợp vào chỗ chấm : 5 km314m =....km , 4m vuông 6 dm vuông =.... m vuông , 2\5 viết dứơi dạng số thập phân là ..... , 25℅ của 1 giờ là ....... phút mình đang cần khẩn cấp nhờ các bạn làm cho mình tí
Đối với mỗi phương trình sau, hãy tìm giá trị của m để phương trình có nghiệm, tính nghiệm của phương trình theo m:
a. mx2 + (2m – 1)x + m + 2 = 0 b. 2x2 - (4m +3)x + 2m2 - 1 = 0
c. x2 – 2(m + 3)x + m2 + 3 = 0 d. (m + 1)x2 + 4mx + 4m +1 = 0
\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Biết rằng khi m có giá trị
m
m
o
thì phương trình sau đây
2
sin
2
x
-
5
m
+
1
sin
x
+
2
m
2
+
2
m
0
có đúng 5 nghiệm phân biệt thuộc khoảng
-...
Đọc tiếp
Biết rằng khi m có giá trị m = m o thì phương trình sau đây 2 sin 2 x - 5 m + 1 sin x + 2 m 2 + 2 m = 0 có đúng 5 nghiệm phân biệt thuộc khoảng - π 2 ; 3 π . Mệnh đề nào sau đây là mệnh đề đúng?
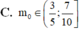
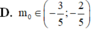
Đáp án D
Tất nhiên đến đây mà vội vàng kết luận thì chưa hoàn thành, các em có thể dễ thấy trường hợp còn lại không có m thỏa mãn yêu cầu bài toán.
Trường hợp phương trình (*) có một nghiệm t 1 = 1 (có hai nghiệm x) và một nghiệm - 1 < t 2 ≤ 0 (có ba nghiệm x).
Rất dễ để tìm được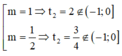 
nhưng rõ ràng không có m theo yêu cầu.
Vậy ta kết luận 
thỏa mãn yêu cầu bài toán và 
.
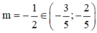§ Bổ trợ kiến thức: Không dễ để các em có thể nhận ra cả 2 trường hợp này trong cùng một bài toán, cho nên khi gặp một số trường hợp đã giải ra kết quả mà có khả năng là đáp án đúng cao thì các em nên mạnh dạn bỏ hẳn trường hợp còn lại để tránh việc mất nhiều thời gian vào các trường hợp không đâu, ở đây phương án bên dưới cho rất nhẹ nên các em có thể dễ dàng kết luận luôn 
và chọn đáp án đúng.
Đúng 0
Bình luận (0)
Biết rằng khi m có giá trị
m
m
o
thì phương trình sau đây
2
sin
2
x
-
5
m
+
1
sin
x
+
2
m
2
+
2
m
0...
Đọc tiếp
Biết rằng khi m có giá trị m = m o thì phương trình sau đây 2 sin 2 x - 5 m + 1 sin x + 2 m 2 + 2 m = 0 có đúng 5 nghiệm phân biệt thuộc khoảng - π 2 ; 3 π . Mệnh đề nào sau đây là mệnh đề đúng?
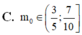
Chọn D
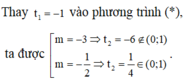
Tất nhiên đến đây mà vội vàng kết luận thì chưa hoàn thành, các em có thể dễ thấy trường hợp còn lại không có m thỏa mãn yêu cầu bài toán
Trường hợp phương trình(*) có một nghiệm t 1 = 1 (có hai nghiệm x) và một nghiệm - 1 < t 2 ≤ 0 (có ba nghiệm x).
Rất dễ để tìm được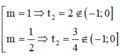 
nhưng rõ ràng không có m theo yêu cầu.
Vậy ta kết luận
m
=
-
1
2
thỏa mãn yêu cầu bài toán và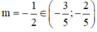 
.
§ Bổ trợ kiến thức: Không dễ để các em có thể nhận ra cả 2 trường hợp này trong cùng một bài toán, cho nên khi gặp một số trường hợp đã giải ra kết quả mà có khả năng là đáp án đúng cao thì các em nên mạnh dạn bỏ hẳn trường hợp còn lại để tránh việc mất nhiều thời gian vào các trường hợp không đâu, ở đây phương án bên dưới cho rất nhẹ nên các em có thể dễ dàng kết luận luôn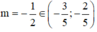 
và chọn đáp án đúng.
Đúng 0
Bình luận (0)