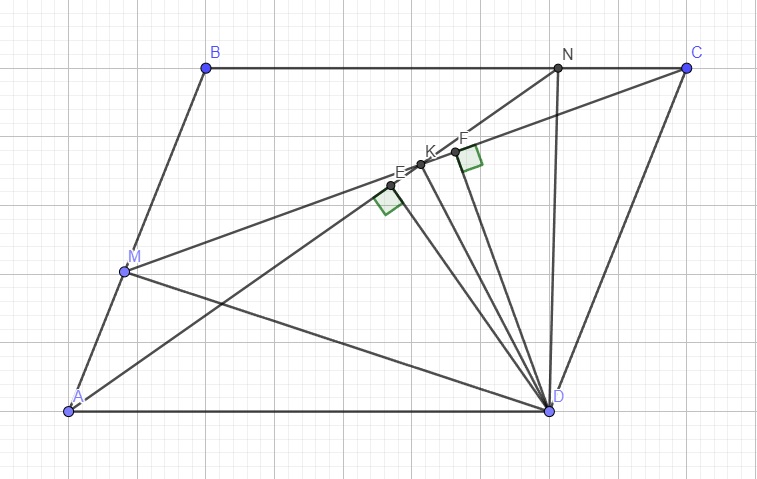
Cho hình bình hành ABCD. Trên cạnh AB và BC lần lượt lấy hai điểm M và N sao cho AN=CM. Gọi K là giao điểm của AN và CM. CMR: KD là tia phân giác của góc AKC

Những câu hỏi liên quan
Cho hình bình hành ABCD. Trên cạnh AB và BC lần lượt lấy hai điểm M và N sao cho AN=CM. Gọi K là giao điểm của AN và CM. CMR: KD là tia phân giác \(\widehat{AKC}\)
Cho hình bình hành ABCD , trên cạnh AB lấy điểm M , trên cạnh BC lấy điểm N sao cho AN CM. Gọi giao điểm của AN và CM là K . Chứng minh KD là tia phân giác của góc AKC.
Đọc tiếp
Cho hình bình hành ABCD , trên cạnh AB lấy điểm M , trên cạnh BC lấy điểm N sao cho AN = CM. Gọi giao điểm của AN và CM là K . Chứng minh KD là tia phân giác của góc AKC.
Trước hết ta chứng minh bổ đề sau (nếu em chưa học)
Cho 4 điểm A; B; C; D phân biệt sao cho \(AB||CD\), khi đó ta luôn có: \(S_{\Delta ACD}=S_{\Delta BCD}\)
C/m: từ A và B lần lượt kẻ \(AH\) và \(BK\) vuông góc CD \(\Rightarrow AH||BK\Rightarrow\) tứ giác AHKB là hình chữ nhật
\(\Rightarrow AH=BK\)
Do \(\left\{{}\begin{matrix}S_{\Delta ACD}=\dfrac{1}{2}AH.CD\\S_{\Delta BCD}=\dfrac{1}{2}BK.CD\end{matrix}\right.\) mà \(AH=BK\Rightarrow S_{\Delta ACD}=S_{\Delta BCD}\) (đpcm)
Quay lại bài toán, áp dụng bổ đề trên ta có: do N thuộc BC nên \(NC||AD\Rightarrow S_{\Delta NAD}=S_{\Delta CAD}\) (1)
Tương tự, \(AM||CD\Rightarrow S_{\Delta ACD}=S_{\Delta MCD}\) (2)
(1);(2) \(\Rightarrow S_{\Delta NAD}=S_{\Delta MCD}\)
Từ D lần lượt kẻ \(DE\perp AN\) và \(DF\perp CM\)
\(\Rightarrow\left\{{}\begin{matrix}S_{\Delta NAD}=\dfrac{1}{2}DE.AN\\S_{\Delta MCD}=\dfrac{1}{2}DF.CM\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}S_{\Delta NAD}=S_{\Delta MCD}\\AN=CM\end{matrix}\right.\) \(\Rightarrow DE=DF\)
\(\Rightarrow\Delta_VDEK=\Delta_VDFK\left(ch-cgv\right)\)
\(\Rightarrow\widehat{EKD}=\widehat{FKD}\) hay KD là phân giác
Đúng 2
Bình luận (0)
Cho hình bình hành ABCD .Gọi điểm M,N lần lượt trên AB,BC sao cho AN=CM.Gọi K là giao điểm của AN và CM.Chứng minh rằng KD là tia phân giác góc AKC
cho hình bình hành ABCD , các điểm M, N theo thứ tự thuộc các cạnh AB, BC sao cho AN=CM , gọi K là giao điểm của AN và CM . chúng minh rằng KD là tia phân giác cảu góc AKD
cho hình bình hành ABCD.Các điểm M,N theo theo thứ tự thuộc các cạnh AB,BC sao cho AN=CM .Gọi K là giao điểm của AN và CM.CMR KD là tia phân giác của \(\widehat{AKC}\)
CHo HBH ABCD . các điểm M , N theo thứ tự thuộc các cạnh AB ; BC sao cho AN = CM . GỌi K là giao điểm AN và CM . CMR KD là tia p/s góc AKC
dạ em chưa học anh ạ .
ai chưa học đến thì cho mình nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. Cho tam giác ABC (A=90 độ) (AB<AC), trên cạnh BC lấy N sao cho BN=NA, trên cạnh BC lấy M sao cho CM=CA. Tia phân giác góc ABC cắt AM tại E, tia phân giác góc ACB cắt AN tại D. Gọi O là giao của BE và CD, gọi H là giao của MD và NE.
a) Tính góc MAN
b) CHứng minh EODH là hình bình hành
c) Gọi K và I lần lượt là trung điểm của AH và MN. Chứng minh IEKD là hình vuông.
Cho hbh ABCD. Các điểm M,N thuộc các cạnh AB,BC sao cho AN=CM. Gọi K là gđ của AM,CN.
a) CMR: S tam giác AND=1/2 S hbh ABCD
b)CMR: KD là tia phân giác của AKC
Kẻ DI,DJ lần lượt vuông góc với AK,CK
\(a,S_{AND}=\dfrac{1}{2}AN\cdot DI=\dfrac{1}{2}S_{ABCD}\) (chung đáy AD, cùng chiều cao hạ từ N)
\(b,S_{CDM}=\dfrac{1}{2}CM\cdot DJ=\dfrac{1}{2}S_{ABCD}\) (chung đáy CD, cùng chiều cao hạ từ M)
\(\Rightarrow\dfrac{1}{2}AN\cdot DI=\dfrac{1}{2}CM\cdot DJ\Rightarrow DI=DJ\left(AN=CM\right)\\ \Rightarrow\Delta DIK=\Delta DJG\left(ch-cgv\right)\\ \Rightarrow\widehat{IKD}=\widehat{JKD}\)
Vậy KD là phân giác \(\widehat{AKC}\)
Đúng 1
Bình luận (0)
Cho hbh ABCD. Các điểm M,N thuộc các cạnh AB,BC sao cho AN=CM. Gọi K là gđ của AM,CN.
a) CMR: S tam giác AND=1/2 S hbh ABCD
b)CMR: KD là tia phân giác của AKC