a: Để hàm số đồng biến thì m-3>0

=>m>3

Để hàm số nghịch biến thì m-3<0

=>m<3

b: Thay x=3 và \(y=\sqrt{3}\) vào (d), ta được:

\(3\left(m-3\right)+\sqrt{2}=\sqrt{3}\)

=>\(3\left(m-3\right)=\sqrt{3}-\sqrt{2}\)

=>\(m-3=\dfrac{\sqrt{3}-\sqrt{2}}{3}\)

=>\(m=\dfrac{\sqrt{3}-\sqrt{2}+9}{3}\)

a) Ta có: \(y=\sqrt{m-3}\cdot x+\dfrac{2}{3}\left(m\ge3\right)\) 

Để đây là hàm số bậc nhất thì: \(\sqrt{m-3}\ne0\Leftrightarrow m=3\) 

Do: \(\sqrt{m-3}\ge0\forall m\ge3\) 

Nên với \(m\ge3\) thì y đồng biến trên R 

b) Ta có: \(y=\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\cdot x+2010\left(m\ge0;m\ne5\right)\)

Để đây là hàm số bậc nhất thì: \(\sqrt{m}-\sqrt{5}\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m\ne5\end{matrix}\right.\) 

Do \(\sqrt{m}+\sqrt{5}>0\Rightarrow\sqrt{m}-\sqrt{5}< 0\Leftrightarrow m< 5\)

Vậy với 0 ≤ m < 5 thì y nghịch biến trên R

a) Để hàm số là hàm số bậc nhất thì:

√(m - 3) > 0

⇔ m - 3 > 0

⇔ m > 3

Vậy với m > 3 thì hàm số đã cho là hàm bậc nhất

b) Để hàm số là hàm bậc nhất thì √m - √5 ≠ 0 và m ≥ 0

⇔ √m ≠ √5

⇔ m ≠ 5

Vậy m ≠ 5 và m ≥ 0 thì hàm số đã cho làm hàm số bậc nhất

*) Để hàm số ở câu a là hàm đồng biến thì m > 3

*) Để hàm số ở câu b là hàm nghịch biến thì √m < √5

⇔ 0 \(\le\) m < 5

Vậy 0 \(\le\) m < 5 thì hàm số ở câu b là hàm số nghịch biến

a: Thay x=1 và y=1 vào (d), ta được:

m+3=1

hay m=-2

b: Vì (d)//y=-2x+3 nên a=-2

Vậy: (d): y=-2x+b

Thay x=0 và y=-3 vào (d), ta được:

b=-3

\(\Leftrightarrow\sqrt{2t^2+mt-m-1}=t-1\) có 2 nghiệm thỏa mãn \(1\le t< 3\)

\(\Rightarrow2t^2+mt-m-1=t^2-2t+1\)

\(\Leftrightarrow f\left(t\right)=t^2+\left(m+2\right)t-m-2=0\) có 2 nghiệm \(1< t_1< t_2< 3\) (hiển nhiên \(t=1\) ko là nghiệm)

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=\left(m+2\right)^2+4\left(m+2\right)>0\\f\left(1\right)=1>0\\f\left(3\right)=9+3\left(m+2\right)-m-2>0\\1< \dfrac{t_1+t_2}{2}=\dfrac{-m-2}{2}< 3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(m+2\right)\left(m+6\right)>0\\2m+13>0\\2< -m-2< 6\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>-2\\m< -6\end{matrix}\right.\\m>-\dfrac{13}{2}\\-8< m< -4\end{matrix}\right.\) \(\Rightarrow-\dfrac{13}{2}< m< -6\)

a: Thay x=1 và y=1 vào (d), ta được:

m+3=1

hay m=-2

b: Vì (d)//y=-2x+3 nên a=-2

Vậy: (d): y=-2x+b

Thay x=0 và y=-3 vào (d), ta được:

b=-3

a: Để hàm số y=(m-1)x+3 đồng biến trên R thì m-1>0

=>m>1

Để hàm số y=(m-1)x+3 nghịch biến trên R thì m-1<0

=>m<1

b: Thay m=3 vào (d), ta được:

\(y=\left(3-1\right)x+3=2x+3\)

Vẽ đồ thị:

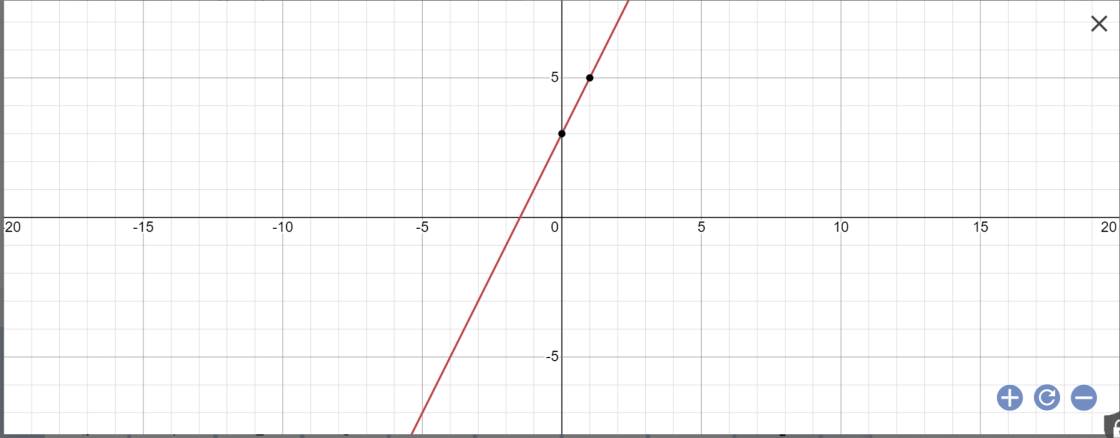
c: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=2\\3\ne-1\left(đúng\right)\end{matrix}\right.\)

=>m-1=2

=>m=3

d: Thay x=-2 và y=0 vào (d1), ta được:

\(-2\left(m-1\right)+3=0\)

=>-2(m-1)=-3

=>\(m-1=\dfrac{3}{2}\)

=>\(m=\dfrac{3}{2}+1=\dfrac{5}{2}\)