Gọi R là điểm trên tia Px, gọi S là điểm trên tia Py sao cho PR = PS. Chứng minh rằng ∠SRX = ∠RSy.

Những câu hỏi liên quan
Cho mXn, trên Xm xác định 2 điểm P,Q trên Xn xác định 2 điểm R và S sao cho XP = XR, XQ = XS
a. Chứng minh rằng tam giác XPS = tam giác XRQ
b. Gọi H là giao điểm của PS và RQ
chứng minh: tam giác PHQ = tam giác RHS
c.chứng minh XH là tia phân giác mXn
a: Xét ΔXPS và ΔXRQ có
XP=XR
\(\widehat{PXS}\) chung
XS=XQ
Do đó: ΔXPS=ΔXRQ
b: ΔXPS=ΔXRQ
=>\(\widehat{XPS}=\widehat{XRQ};\widehat{XSP}=\widehat{XQR}\)
\(\widehat{XPS}+\widehat{SPQ}=180^0\)
\(\widehat{XRQ}+\widehat{SRQ}=180^0\)
mà \(\widehat{XPS}=\widehat{XRQ}\)
nên \(\widehat{SPQ}=\widehat{SRQ}\)
XP+PQ=XQ
XR+RS=XS
mà XP=XR và XQ=XS
nên PQ=RS
Xét ΔHPQ và ΔHRS có
\(\widehat{HPQ}=\widehat{HRS}\)
PQ=RS
\(\widehat{HQP}=\widehat{HSR}\)
Do đó: ΔHPQ=ΔHRS
c: ΔHPQ=ΔHRS
=>HP=HR và HQ=HS
Xét ΔXHQ và ΔXHS có
XH chung
HQ=HS
XQ=XS
Do đó:ΔXHQ=ΔXHS
=>\(\widehat{QXH}=\widehat{SXH}\)
=>XH là phân giác của \(\widehat{mXn}\)
Đúng 1
Bình luận (0)
Từ một điểm P nằm trên cạnh đáy BC của tam giác ABC vẽ các tia Px, Py song song với các cạnh AB, AC cắt AC tại Q, R. Gọi D là điểm đối xứng với P qua QR. Chứng minh rằng D nằm trên đường tròn ngoại tiếp tam giác ABC
cho đoạn thẳng PQ=4cm.lấy điểm R trên tia PQ sao cho PR=6cm
a. tính độ dài đoạn thẳng QR
b. gọi K là trung điểm của đoạn thẳng PQ. chứng minh rằng Q là trung điểm của KR
a)Tính QR
Điểm Q nằm giữa 2 điểm R và P
QR+QP=PR
QR+4=6
QR=6-4=2
b)TÍNH PK và KQ
Điểm K là Trung điểm của đoạn PQ
KQ=KP=PQ:2=4:2=2
Điểm Q là TRUNG ĐIỂM CỦA ĐOẠN KR
vì :+Vì điểm Q nằm giũa 2 điểm K và R
+QK=QR=2CM
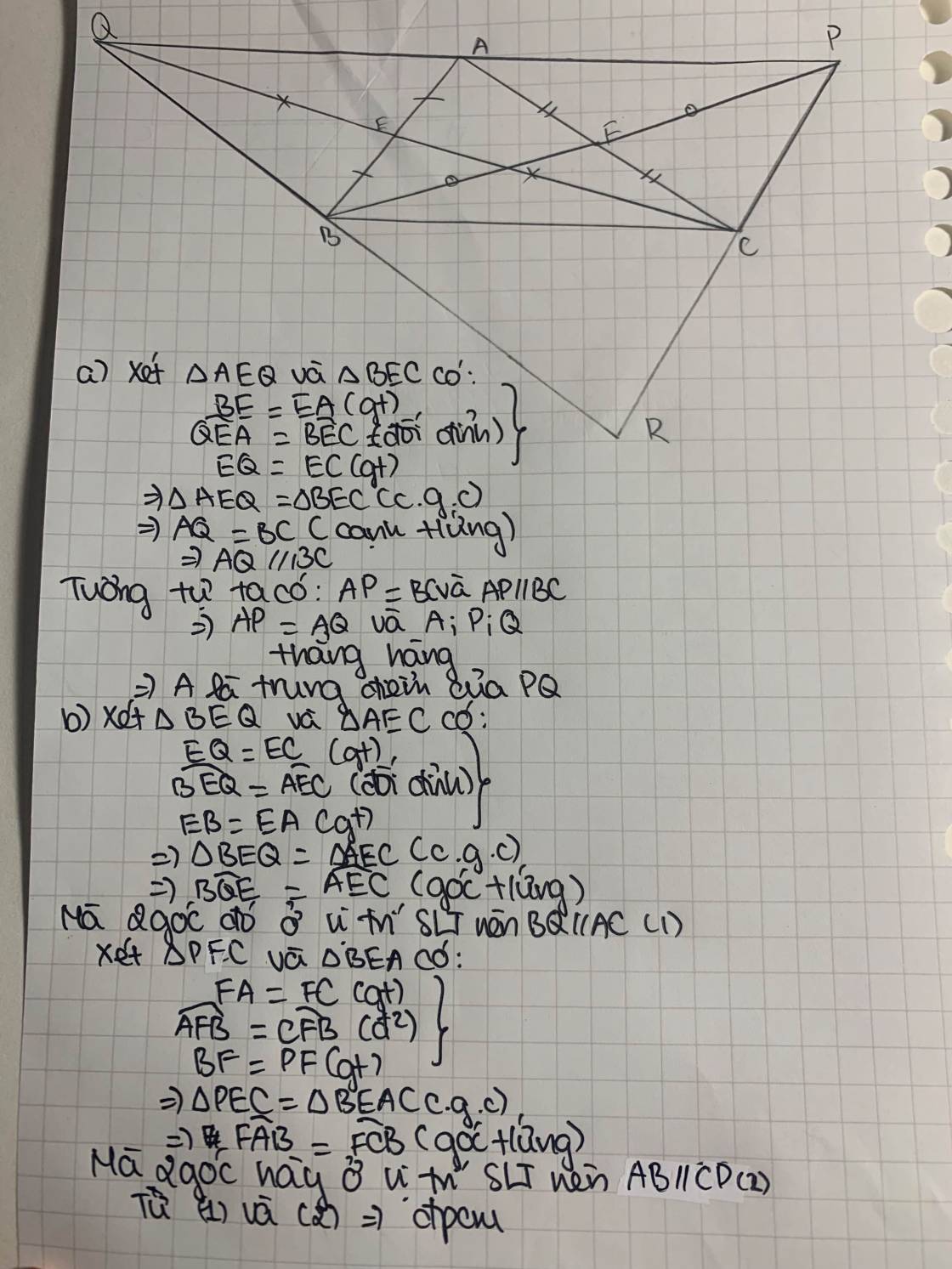
Cho tam giác ABC. Gọi E, F lần lượt là trung điểm của AB, AC. Trên tia đối của tia FB lấy P sao cho PF BF. Trên tia đối của tia EC lấy điểm Q sao cho QE CE.
a) Chứng minh A là trung điểm của PQ.
b) Chứng minh BQ // AC và CP // AB.
c) Gọi R là giao điểm của hai đường thẳng PC và QB. Chứng minh chu vi tam giác PQR bằng hai lần chu vi tam giác ABC.
d) Chứng minh AR, BP,CQ đồng quy tại một điểm.
Đọc tiếp
Cho tam giác ABC. Gọi E, F lần lượt là trung điểm của AB, AC. Trên tia đối của tia FB lấy P sao cho PF = BF. Trên tia đối của tia EC lấy điểm Q sao cho QE = CE.
a) Chứng minh A là trung điểm của PQ.
b) Chứng minh BQ // AC và CP // AB.
c) Gọi R là giao điểm của hai đường thẳng PC và QB. Chứng minh chu vi tam giác PQR bằng hai lần chu vi tam giác ABC.
d) Chứng minh AR, BP,CQ đồng quy tại một điểm.
Trên tia Px lấy các điểm A,B,C sao cho PA=5cm: PB=8cm,PC=11cm. tính đoạn BC.
a Chứng minh b là trung điểm của đoạn AC
b Lấy M thuộc tia đối của tia Px sao cho PM=3cm. Gọi k là trung điểm của MC. Tính KC
Ta có: PB < PC ( 8cm < 11cm )
=) B nằm giữa P và C
=) PB + BC = PC
Thay PB = 8cm, PC = 11cm, ta có :
8 + BC = 11 =) BC = 11 - 8 =) BC = 3 (cm)
Vậy độ dài đoạn BC là 3cm.
a) Ta có: PA < PB ( 5cm < 8cm )
=) A nằm giữa P và B
=) AP + AB = PB
Thay AP = 5cm, PB = 8cm, ta có:
5 + AB = 8 =) AB = 8 - 5 =) AB = 3 (cm)
Mà AB = BC = 3cm
=) B là trung điểm của đoạn AC (đpcm)
b) Ta có: PM + PC = MC ( M thuộc tia đối tia Px )
Thay PM = 3cm, PC = 11cm, ta có:
PM + PC = MC =) CM = 3 + 11 =) MC= 14 (cm)
Mà K là trung điểm MC =) 2.KC = MC
Thay MC = 14cm, ta có
KC = \(\frac{14}{2}\)=) KC = 7 (cm)
Vậy độ dài KC là 7cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB =AC . Gọi M là trung điểm của đoạn thẳng BC .
a) Chứng minh rằng ΔABM =ΔACM .
b) Trên tia đối của tia MA lấy điểm D sao cho MD = MA . Chứng minh rằng AB // CD .
c) Gọi I là trung điểm của đoạn thẳng BD . Trên tia đối của tia IC lấy điểm E sao cho
IE =IC . Chứng minh rằng A B E , thẳng hàng.
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Đúng 1
Bình luận (1)
Cho tam giác ABC, M trung điểm BC. Trên tia đối tia MA lấy điểm E sao cho ME = MA. Gọi I là một điểm trên AC, K là 1 điểm trên EB sao cho AI = EK.
a)Chứng minh rằng: tam giác AMC = EMB
b) chứng minh rằng: AB//EC.
c) Chứng minh rằng: Ba điểm I,M,K thẳng hàng.
Cho tam giác ABC, M trung điểm BC. Trên tia đối tia MA lấy điểm E sao cho ME = MA. Gọi I là một điểm trên AC, K là 1 điểm trên EB sao cho AI = EK.
a)Chứng minh rằng: tam giác AMC = EMB
b) chứng minh rằng: AB//EC.
c) Chứng minh rằng: Ba điểm I,M,K thẳng hàng.
b: Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//EC
Đúng 0
Bình luận (0)
Cho tam giác ABC, M trung điểm BC. Trên tia đối tia MA lấy điểm E sao cho ME = MA. Gọi I là một điểm trên AC, K là 1 điểm trên EB sao cho AI = EK.
a)Chứng minh rằng: tam giác AMC = EMB
b) chứng minh rằng: AB//EC.
c) Chứng minh rằng: Ba điểm I,M,K thẳng hàng.
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC
Đúng 3
Bình luận (0)
\(a,\left\{{}\begin{matrix}AM=ME\\BM=MC\\\widehat{AMC}=\widehat{BME}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta AMC=\Delta EMB\left(c.g.c\right)\\ b,\left\{{}\begin{matrix}AM=ME\\BM=MC\\\widehat{AMB}=\widehat{CME}\left(đđ\right)\end{matrix}\right.\Rightarrow\Delta AMB=\Delta EMC\left(c.g.c\right)\\ \Rightarrow\widehat{MAB}=\widehat{MEC}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}EC\\ c,\left\{{}\begin{matrix}\widehat{MAI}=\widehat{MEK}\\AM=ME\\KE=AI\end{matrix}\right.\Rightarrow\Delta AMI=\Delta EMK\left(c.g.c\right)\\ \Rightarrow\widehat{AMI}=\widehat{EMK}\\ \text{Mà 2 góc này ở vị trí đối đỉnh và }A,M,E\text{ thẳng hàng nên }I,M,K\text{ thẳng hàng}\)
Đúng 2
Bình luận (0)