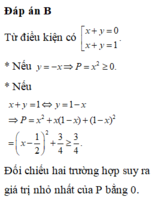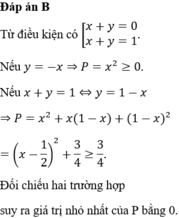P=x2+xy+y2-3y-3x+16 Tìm giá trị nhỏ nhất

Những câu hỏi liên quan
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức
P
x...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P = x 2 + x y + y 2 bằng
A. 3 4
B. 0
C. 1 4
D. 1 2
Cho các số thực x, y thoả mãn
2
x
+
y
-
1
(
3
x
+
y
+
1
)
3
x
+
3
y
+
1
. Giá trị nhỏ nhất của biểu thức P
x
2
+
x
y...
Đọc tiếp
Cho các số thực x, y thoả mãn 2 x + y - 1 ( 3 x + y + 1 ) = 3 x + 3 y + 1 . Giá trị nhỏ nhất của biểu thức P= x 2 + x y + y 2 bằng
A. 3 4
B. 0.
C. 1 4
D. 1 2
Tìm giá trị nhỏ nhất:
a/ P=x2+y2-6x-2y+17
b/ Q=x2+xy+y2-3x-3y+999
c/ R=2x2+2xy+y2-2x+2y+15
d/ S=x2+26y2-10xy+14x-76y+59
e/ T=x2-4xy+5y2+10x-22y+28
Giúp mình với nha!
Tìm giá trị nhỏ nhất của biểu thức x2+y2+z2-yz-4x-3y+2018
tìm giá trị nhỏ nhất của biểu thức
A = x2 + y2 +z2 - yz - 4x - 3y + 2027
\(A=x^2+y^2+z^2-yz-4x-3y+2027\)
\(\Rightarrow4A=4x^2+4y^2+4z^2-4yz-16x-12y+8108=4x^2-16x+16+3y^2+12y+12+y^2-4yz+4z^2+8080=4\left(x-2\right)^2+3\left(y+2\right)^2+\left(y-2z\right)^2+8080\)
Vì \(4\left(x-2\right)^2\ge0\)
\(3\left(y+2\right)^2\ge0\)
\(\left(y-2z\right)^2\ge0\)
\(\Rightarrow4A\ge8080\Rightarrow A\ge2020\)
\(ĐTXR\Leftrightarrow x=2,y=-2,z=-1\)
Đúng 4
Bình luận (0)
Cho x2+y2=6 .
a)Tìm giá trị nhỏ nhất của A=x 4+y4
b) Tìm giá trị lớn nhất của B=x+y; C=xy
Lời giải:
a. Áp dụng BĐT Cô-si:
$x^4+9\geq 6x^2$
$y^4+9\geq 6y^2$
$\Rightarrow x^4+y^4+18\geq 6(x^2+y^2)$
$A+18\geq 36$
$A\geq 18$
Vậy GTNN của $A$ là $18$ khi $x^2=y^2=3$
b.
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 2(x^2+y^2)\geq (x+y)^2$
$\Leftrightarrow 12\geq (x+y)^2$
$\Rightarrow B=x+y\leq \sqrt{12}$. Vậy $B$ max bằng $\sqrt{12}$ khi $x=y=\sqrt{3}$
$(x-y)^2\geq 0$
$\Leftrightarrow x^2+y^2\geq 2xy$
$\Leftrightarrow 6\geq 2C$
$\Leftrightarrow C\leq 3$. Vậy $C_{\max}=3$. Giá trị này đạt tại $x=y=-\sqrt{3}$
Đúng 0
Bình luận (0)
Tim x : (x^4+2x^3+10x+25) : (x^2 + 5)=3
tìm giá trị nhỏ nhất của biểu thức P=x^2 + xy + y^2 - 3x -3y+16
Biết x2+4y2+9z2=3 Tìm GTLN của S=2x+4y+6x
Cho x;y ∈ 𝑅 thỏa mãn x2+y2 -xy=4 . Tìm giá trị lớn nhất và nhỏ nhất của C= x2+y2
a) Áp dụng bất đẳng thức Cosi ta có :
\(x^2+1\geq 2x\\ 4y^2+1\geq 4y\\ 9z^2+1\geq 6z\)
Suy ra \(S\leq 6\)
Dấu = xảy ra khi \(x=1;y=\frac{1}{2}; z=\frac{1}{3}\)
Đúng 0
Bình luận (0)
Câu 14. Cho biểu thức P x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:x2 + 4y2 + z2 – 2a + 8y – 6z + 15 0Câu 16. Tìm giá trị lớn nhất của biểu thức:Câu 17. So sánh các số thực sau (không dùng máy tính):Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3Câu 19. Giải phương trình: .Câu 20. Tìm giá trị lớn nhất của biểu thức A x2y với các điều kiện x, y 0 và 2x + x...
Đọc tiếp
Câu 14. Cho biểu thức P = x2 + xy + y2 – 3(x + y) + 3. Chứng minh rằng giá trị nhỏ nhất của P bằng 0.
Câu 15. Chứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
Câu 16. Tìm giá trị lớn nhất của biểu thức:![]()
Câu 17. So sánh các số thực sau (không dùng máy tính):
Câu 18. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3
Câu 19. Giải phương trình: ![]() .
.
Câu 20. Tìm giá trị lớn nhất của biểu thức A = x2y với các điều kiện x, y > 0 và 2x + xy = 4.
Câu 21. Cho ![]() .
.
Hãy so sánh S và ![]() .
.
Câu 22. Chứng minh rằng: Nếu số tự nhiên a không phải là số chính phương thì √a là số vô tỉ.
Câu 23. Cho các số x và y cùng dấu. Chứng minh rằng:
Câu 24. Chứng minh rằng các số sau là số vô tỉ:
Câu 25. Có hai số vô tỉ dương nào mà tổng là số hữu tỉ không?
Câu 26. Cho các số x và y khác 0. Chứng minh rằng:
![]()
Câu 27. Cho các số x, y, z dương. Chứng minh rằng:
![]()
Câu 28. Chứng minh rằng tổng của một số hữu tỉ với một số vô tỉ là một số vô tỉ.
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 29:
a: \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\)
\(\Leftrightarrow-a^2+2ab-b^2\le0\)
\(\Leftrightarrow-\left(a-b\right)^2\le0\)(luôn đúng)
Đúng 1
Bình luận (0)