choΔABC.Trên nửa mặt phẳng bờ AC không chứa điểm B,Vẽ tam giác ADC sao cho
AD=BC,DC=AB
chứng minh
a)góc BAC=gócACD từ đó chứng tỏ AB song song với DC
b)AD có son song với BC không?Vì sao
c)Kẻ AH⊥DC tại H.Chứng tỏ AH⊥AB
choΔABC.Trên nửa mặt phẳng bờ AC không chứa điểm B,Vẽ tam giác ADC sao cho
AD=BC,DC=AB
chứng minh
a)góc BAC=gócACD từ đó chứng tỏ AB song song với DC
b)AD có son song với BC không?Vì sao
c)Kẻ AH⊥DC tại H.Chứng tỏ AH⊥AB
c) Theo câu a) ta có \(\Delta ABC=\Delta CDA.\)
=> \(\widehat{ABC}=\widehat{CDA}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AB\) // \(CD.\)
Vì:
\(AH\perp CD\left(gt\right)\)
\(AB\) // \(CD\left(cmt\right)\)
=> \(AH\perp AB\left(đpcm\right).\)
Hình vẽ của mình thì hơi sai nhé là \(AH\perp BC\) vì có bài cũng gần giống của bạn nên mình lấy hình này.
Chúc bạn học tốt!
choΔABC.Trên nửa mặt phẳng bờ AC không chứa điểm B,Vẽ tam giác ADC sao cho
AD=BC,DC=AB
chứng minh
a)góc BAC=gócACD từ đó chứng tỏ AB song song với DC
b)AD có son song với BC không?Vì sao
c)Kẻ AH⊥DC tại H.Chứng tỏ AH⊥AB
Cho tam giác ABC ( AB<AC) . Trên tia AB lấy điểm D sao cho AD = AC. Kẻ phân giác AM của BAC ( M thuộc DC)
1/ Chứng Minh DK=CK ( K Là giao điểm của BC và AM)
2/Kẻ BH vuông góc với DC ( H thuộc DC) . Chứng Minh HB//AM
3/Qua A kẻ đường thẳng Xy song song với DC. Trên nửa mặt phẳng bờ là AM không chứa điểm C, lấy điểm Q thuộc Xy sao cho AQ=HM. Chứng minh ba điểm Q, H, B thẳng hàng
Cho tam giác ABC, kẻ AH vuông góc với BC. Trên nửa mặt phẳng AC không chứa điểm B và tam giác ACD sao cho AD=BC, CD=AB. Chứng minh:
a) AB song song với CD
b) AH vuông góc với AD
a) Xét tam giác BAC và tam giác DAC:
AB = CD (gt)
AD = BC (gt)
AC chung
=> tam giác BAC = tam giác DAC (c.c.c) => góc BAC = góc ACD mà 2 óc này ở vị trí so le trong nên suy ra AB // CD (đpcm).
b) Ta có: tam giác BAC = tam giác DAC (chứng minh trên) => góc DAC = góc ACB mà 2 góc này ở vị trí so le trong nên suy ra AD // BC.
Ta lại có: AH vuông góc với BC (gt)
AD // BC (chứng minh trên)
=> AH vuông góc với AD (đpcm).
Giải:
a) Xét \(\Delta BAC,\Delta DCA\) có:
\(AD=BC\left(gt\right)\)
\(CD=AB\left(gt\right)\)
AC: cạnh chung
\(\Rightarrow\Delta BAC=\Delta DAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\) ( góc t/ứng )
mà 2 góc trên ở vị trí so le trong nên AB // CD và AD // BC
b) Vì \(AH\perp BC\) và AD // BC nên \(AH\perp AD\)
Vậy...
Cho tam giác ABC, đường cao AH. Trên nửa mặt phẳng bờ AC không chứa điểm B, vẽ tam giác ACD sao cho AD = BC, CD = AB. Chứng minh rằng AB song song CD và AH vuông góc AD.
xét tam giác ABC và tam giác CDA có AB=CD;BC=AD;AD chung
=>tam giác ABC=tam giác CDA
=>góc ACB=góc DAC(2 góc tương ứng)
mà 2 góc này có vị trí so le trong nên AB//CD
mà AH vuông góc BC nên AH vuông góc CD
cho tam giác ABC có AB = AC. Tia phân giác A cắt BC ở D. a) Chứng minh tam giác ABD = tam giác ACD và BD = DC b) chứng minh AD vuông với BC c) trên nửa mặt phẳng không chứa điểm A bờ là đường thẳng BC vẽ tia Bx song song với AC. Trên cạnh AC lấy điểm E, trên tia Bx. Lấy điểm N sao cho CE = BN. Chứng minh ba điểm N,D,E thẳng hàng
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
Suy ra: BD=CD
b: Ta có: ΔABC cân tại A
mà AD là tia phân giác
nên AD là đường cao
Cho tam giác ABC. Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB, vẽ tia AD sao cho B A D ^ = A B C ^ . Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia AE sao cho C A E ^ = A C B ^ . Chứng minh.:
a) AD song song với BC;
b) Ba điểm D, A, E thẳng hàng
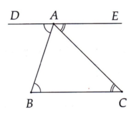
a) Có B A D ^ = A B C ^ ( giả thiết),
Mà hai góc ở vị trí so le trong nên AD // BC (theo tính chất hai đường thẳng song song).
b) Tương tự ý a), chứng minh được AE // BC
Theo tiên đề ơ-clit, hai đường thẳng AE và AD trùng nhau. Từ đó ba điểmD, A, E thẳng hàng.
Cho tam giác ABC. Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB, vẽ tia AD sao cho B A D ^ = A B C ^ . Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia AE sao cho C A E ^ = A C B ^ . Chứng minh.:
a) AD song song với BC;
b) Ba điểm D, A, E thẳng hàng
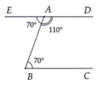
a) Có B A D ^ = A B C ^ ( giả thiết),
Mà hai góc ở vị trí so le trong nên AD // BC (theo tính chất hai đường thẳng song song).
a) Tương tự ý a), chứng minh
b) được AE // BC
Theo tiên đề ơ-clit, hai đường thẳng AE và AD trùng nhau. Từ đó ba điểm D, A, E thẳng hàng
Cho tam giác ABC có AB=AC, AM là tia phân giác của góc A (M thuộc BC)
a) chứng minh: tam giác ABC= tam giác ACM
b) Trên tia đối của tia MA lấy điểm D sao cho MD=MA.chứng minh AB song song với DC
c) Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ đoạn thẳng AE sao cho AE song song với BC và AE=BC. Chứng minh D,C,E thẳng hàng