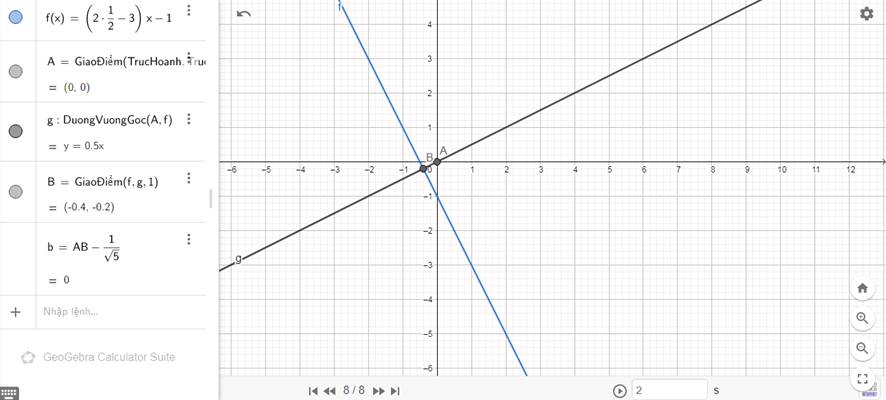
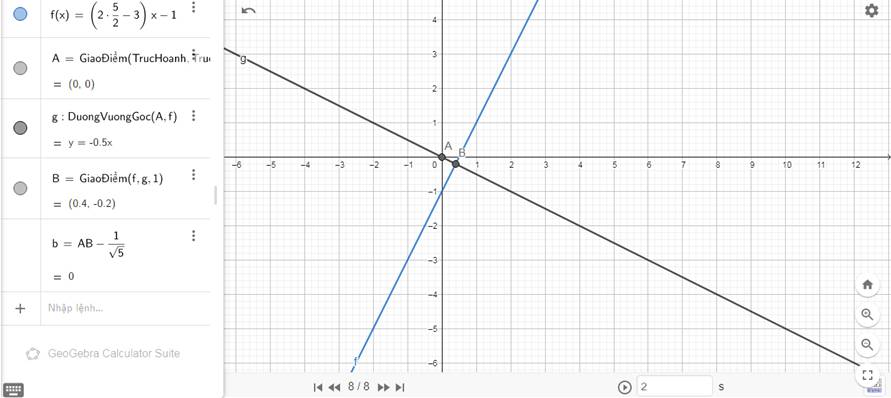
cho (d) : y = (2m - 3)x - 1. Tìm m sao cho khoảng cách từ gốc tọa độ đến (d) = 1/căn 5

Những câu hỏi liên quan
Cho đường thằng d: 2(m-1)x+(m-2)y=3
1. vẽ d với m=3
2.chứng minh d luôn đi qua 1 điểm cô định với mọi m
3. tìm m để d cách gốc tọa độ 1 khoảng lớn nhất
1) bạn tự vẽ nha
d <=> (m-2)y=3-2(m-1)x
2) chọn m=0 <=> -2y=3+2x <=> y=-3/2 -x
chọn m=-1 <=> -3y= 3+4x <=> y=-1-4/3 x
xét pt: \(-\frac{3}{2}-x=-1-\frac{4}{3}x\Leftrightarrow\frac{1}{3}x=\frac{1}{2}\Leftrightarrow x=\frac{1}{6}\Rightarrow y=-\frac{3}{2}-\frac{1}{6}=-\frac{5}{3}\)
=> đt d luôn đi qua một điểm cố định có tọa độ (1/6;-5/3)
3) gọi khoảng cách ấy là h
ta có: \(h=\frac{\left|c\right|}{\sqrt{a^2+b^2}}=\frac{\left|3\right|}{\sqrt{\left(2m-2\right)^2+\left(m-2\right)^2}}=\frac{3}{\sqrt{5m^2-12m+8}}\)
ta có: \(5m^2-12m+8=5\left(m^2-\frac{12}{5}m+\frac{36}{25}\right)+\frac{4}{5}=5\left(m-\frac{6}{5}\right)^2+\frac{4}{5}\ge\frac{4}{5}\Leftrightarrow\sqrt{5m^2-12m+8}\ge\sqrt{\frac{4}{5}}\)
\(\Rightarrow\frac{3}{\sqrt{5m^2-12m+8}}\le\frac{3}{\sqrt{\frac{4}{5}}}=\frac{3\sqrt{5}}{2}\Rightarrow MaxH=\frac{3\sqrt{5}}{2}\Leftrightarrow m=\frac{6}{5}\)
Đúng 0
Bình luận (0)
Vật chuyển động thẳng trên trục Ox từ gốc tọa độ đến điểm M có tọa độ x = 100cm rồi quay trở lại gốc tọa độ, độ biến thiên tọa độ và quãng đường đi được là
Bài 1: Biết đồ thị của hàm số là đường thẳng đi qua gốc tọa độ, hãy xác định hàm số trong mỗi trường hợp saua) Đi qua điểm A( 3; 2)b) Có hệ số a bằng 2c) Song song với đường thẳng y3x+1Bài 2: Cho đường thẳng y(k+1)x+k (1)a) Tìm k để (1) đi qua gốc tọa độ b) Tìm k để (1) cắt truc tung tại điểm có tung độ bằng 1 trừ căn 2c) Tìm k để (1) song song với đường thẳng y ( căn 3 +1)x +3
Đọc tiếp
Bài 1: Biết đồ thị của hàm số là đường thẳng đi qua gốc tọa độ, hãy xác định hàm số trong mỗi trường hợp sau
a) Đi qua điểm A( 3; 2)
b) Có hệ số a bằng 2
c) Song song với đường thẳng y=3x+1
Bài 2: Cho đường thẳng y=(k+1)x+k (1)
a) Tìm k để (1) đi qua gốc tọa độ
b) Tìm k để (1) cắt truc tung tại điểm có tung độ bằng 1 trừ căn 2
c) Tìm k để (1) song song với đường thẳng y = ( căn 3 +1)x +3
cho hàm số y = (2m - 3)x - 1 ( m khác \(\dfrac{3}{2}\)\(\dfrac{ }{ }\)) có đồ thị đường thẳng (d). Tìm giá trị của m sao cho khoảng cách từ gốc tọa độ đến đường thẳng (d) bằng \(\dfrac{1}{\sqrt{5}}\)
- Gọi M(x0,y0) ,N(x1,y1) lần lượt là giao điểm của đường thẳng (d): \(y=\left(2m-3\right)x-1\) với trục tung, trục hoành \(\Rightarrow x_0=y_1=0\).
Vì M(0;y0) thuộc (d) nên: \(y_0=\left(2m-3\right).0-1=-1\)
\(\Rightarrow M\left(0;-1\right)\) nên \(OM=1\) (đvđd)
\(N\left(x_1;0\right)\) thuộc (d) nên: \(\left(2m-3\right)x_1-1=0\Rightarrow x_1=\dfrac{1}{2m-3}\)
\(\Rightarrow N\left(\dfrac{1}{2m-3};0\right)\) nên \(ON=\dfrac{1}{2m-3}\) (đvđd)
*Hạ OH vuông góc với (d) tại H \(\Rightarrow OH=\dfrac{1}{\sqrt{5}}\)
Xét △OMN vuông tại O có OH là đường cao.
\(\Rightarrow\dfrac{1}{OM^2}+\dfrac{1}{ON^2}=\dfrac{1}{OH^2}\)
\(\Rightarrow1+\left(2m-3\right)^2=5\)
\(\Rightarrow2m-3=\pm2\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=\dfrac{1}{2}\end{matrix}\right.\) (nhận)
Đúng 3
Bình luận (1)
Hai nguồn sóng kết hợp cùng pha A, B cách nhau 10cm có bước sóng 1cm. Chọn trục tọa độ xOy với Ox trùng với chiều từ A đến B gốc tọa độ tại A. Đường thẳng d có phương trình y=x. Điểm trên đường thẳng d dao động với biên độ cực đại xa A nhất cách A là
A. 259cm
B. 302cm
C. 175cm
D. 254cm
Cho đường thẳng (D): y= (m-3)x + 2m -1. Tìm m để (D) cắt Ox tại A, cắt Oy tại B sao cho khoảng cách từ O đến AB lớn nhất
Gọi (d) là đồ thị của ham số bậc nhất y=mx+m-m. Tìm m để (d) đi qua gốc tọa độ
Thay x=0 và y=0 vào (d), ta được:
0m+m-m=0
=>0m=0(luôn đúng)
Đúng 0
Bình luận (0)
cho đường thẳng (d) có phương trình y=(2m+1)x-2,(d) cắt Ox tại A, cắt Oy tại B.Tìm m sao cho
a) khoảng cách từ gốc tọa độ O đến đường thẳng (d) là căn 2
b)Diện tích tam giác AOB = 1/2
PT giao Ox, Oy là:
\(y=0\Leftrightarrow x=\dfrac{2}{2m+1}\Leftrightarrow A\left(\dfrac{2}{2m+1};0\right)\Leftrightarrow OA=\dfrac{2}{\left|2m+1\right|}\\ x=0\Leftrightarrow y=-2\Leftrightarrow B\left(0;-2\right)\Leftrightarrow OB=2\)
\(a,\) Gọi H là chân đường cao từ O đến (d) \(\Leftrightarrow OH=\sqrt{2}\)
Ap dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{\left(2m+1\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{\left(2m+1\right)^2}{4}=\dfrac{1}{4}\Leftrightarrow4m^2+4m+1=1\\ \Leftrightarrow4m\left(m+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=-1\end{matrix}\right.\)
\(b,S_{AOB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\Leftrightarrow OB\cdot OA=1\\ \Leftrightarrow\dfrac{2}{\left|2m+1\right|}\cdot2=1\Leftrightarrow\left|2m+1\right|=4\\ \Leftrightarrow\left[{}\begin{matrix}2m+1=4\\2m+1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{3}{2}\\m=-\dfrac{5}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
cho đường thẳng d:y = (2m - 5)x - 1 + m = 0 tìm m sao cho khoảng cách từ o đến d là nhỏ nhất, lớn nhất