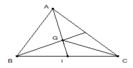
Cho tam giác ABC . D là trung điểm BC Xác định vị trí G biết \(\overrightarrow{AG}=2\overrightarrow{GD}\)

Những câu hỏi liên quan
1. cho \(\Delta ABC\) , D là trung điểm của BC . Xác định vị trí điểm G biết \(\overrightarrow{AG}=2\overrightarrow{GD}\)
\(\overrightarrow{AG}=2\overrightarrow{GD}=2\left(\overrightarrow{GA}+\overrightarrow{AD}\right)=2\overrightarrow{GA}+2\overrightarrow{AD}\)
\(\Rightarrow3\overrightarrow{AG}=2\overrightarrow{AD}\Rightarrow\overrightarrow{AG}=\frac{2}{3}\overrightarrow{AD}\)
\(\Rightarrow G\) là trọng tâm tam giác ABC
Đúng 0
Bình luận (0)
cho tam giác ABC có trọng tâm là G và M là trung điểm BC. Khẳng định nào sau đây là saiA. overrightarrow{AG}dfrac{2}{3}overrightarrow{AM} B. overrightarrow{AB}+overrightarrow{AC}3overrightarrow{AG} C. overrightarrow{GA}overrightarrow{BG}+overrightarrow{GC} D.overrightarrow{GB}+overrightarrow{GC}overrightarrow{GM}giúp mk giải câu C , D thôi cx đc tại cô mk bảo phải cm từng câu cho nên m.n giúp mk vs
Đọc tiếp
cho tam giác ABC có trọng tâm là G và M là trung điểm BC. Khẳng định nào sau đây là sai
A. \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
B. \(\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AG}\)
C. \(\overrightarrow{GA}=\overrightarrow{BG}+\overrightarrow{GC}\)
D.\(\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{GM}\)
giúp mk giải câu C , D thôi cx đc tại cô mk bảo phải cm từng câu cho nên m.n giúp mk vs
c) \(\overrightarrow{BG}+\overrightarrow{GC}=\overrightarrow{BC}\ne\overrightarrow{GA}\)
d) \(\overrightarrow{GB}+\overrightarrow{GC}=\dfrac{1}{2}\overrightarrow{GM}\ne\overrightarrow{GM}\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD tâm O. Xác định vị trí điểm M thỏa mãn \(\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{AM}\). Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và dựng điểm K sao cho \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\). Khi đó, điểm K trùng với
Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P
Đúng 0
Bình luận (0)
Cho tam giác ABC có D là trung điểm BC. Xác định vị trí của G biết
A
G
→
2
G
D
→
A. G là trung điểm BC B.G là hình chiếu của A trên BC C. G là tâm đường tròn ngoại tiếp tam giác D. G là trọng tâm
Đọc tiếp
Cho tam giác ABC có D là trung điểm BC. Xác định vị trí của G biết A G → = 2 G D →
A. G là trung điểm BC
B.G là hình chiếu của A trên BC
C. G là tâm đường tròn ngoại tiếp tam giác
D. G là trọng tâm
Cho tam giác ABC có D là trung điểm BC. Xác định vị trí của G biết
A
G
→
2
G
D
→
A. G là trung điểm BC B. G là hình chiếu của A trên BC C. G là tâm đường tròn ngoại tiếp tam giác D. G là trọng tâm
Đọc tiếp
Cho tam giác ABC có D là trung điểm BC. Xác định vị trí của G biết A G → = 2 G D →
A. G là trung điểm BC
B. G là hình chiếu của A trên BC
C. G là tâm đường tròn ngoại tiếp tam giác
D. G là trọng tâm
Chọn D.
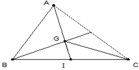
![]() A,G, D thẳng hàng.
A,G, D thẳng hàng.
AG = 2GD và G nằm giữa A và D.
Vậy G là trọng tâm tam giác ABC.
Đúng 0
Bình luận (0)
1.Cho tam giác ABC có D là trung điểm BC. Xác định vị trí của G biết \(\overrightarrow{AG}\)=\(2\overrightarrow{GD}\).
2.Cho 2 điểm A và B. Tìm điểm I sao cho \(\overrightarrow{IA}\)+2\(\overrightarrow{IB}\)=\(\overrightarrow{0}\).
MỌI NGƯỜI GIÚP MÌNH VỚI .
1) AG= 2GA+ 2 AD
AG+ 2AG= 2AD
3 AG= 2AD
AG= 2/3 AD
2) IA + 2 IA+ 2AB=0
3 IA= -2 AB
IA= -2/3 AB
Đúng 0
Bình luận (0)
2: vecto IA+2 vecto IB=vecto 0
=>vecto IA=-2*vecto IB
=>I nằm giữa A và B và IA=2IB
Đúng 0
Bình luận (0)
Cho tứ giác ABCD . Ta gọi G là trọng tâm tứ giác ABCD khi và chỉ khi \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\) . Xác định vị trí G đó
Cho tam giác ABC có G là trọng tâm. Xác định ảnh của tam giác ABC qua phép tịnh tiến theo vectơ \(\overrightarrow{AG}\). Xác định điểm D sao cho phép tịnh tiến theo vectơ \(\overrightarrow{AG}\) biến D thành A ?

- Dựng hình bình hành ABB'G và ACC'G. Khi đó ta có: \(\overrightarrow{AG}=\overrightarrow{BB'}=\overrightarrow{CC'}\)
. Suy ra \(^T\overrightarrow{AG}\left(A\right)=G,^T\overrightarrow{AG}\left(B\right)=B',^T\overrightarrow{AG}\left(C\right)=C'\)
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ \(\overrightarrow{AG}\) là tam giác GB'C'.
- Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có \(\overrightarrow{DA}=\overrightarrow{AG}\). Do đó, \(^T\overrightarrow{AG}\left(D\right)=A\).
Đúng 0
Bình luận (0)

- Dựng hình bình hành ABB'G và ACC'G. Khi đó ta có: −−→AG=−−→BB′=−−→CC′AG→=BB′→=CC′→
. Suy ra T−−→AG(A)=G,T−−→AG(B)=B′,T−−→AG(C)=C′TAG→(A)=G,TAG→(B)=B′,TAG→(C)=C′
Do đó ảnh của tam giác ABC qua phép tịnh tiến theo vectơ −−→AGAG→ là tam giác GB'C'.
- Trên tia GA lấy điểm D sao cho A là trung điểm của GD. Khi đó ta có −−→DA=−−→AGDA→=AG→. Do đó, T−−→AG(D)=ATAG→(D)=A.
Đúng 0
Bình luận (0)
cho ΔABC, gọi G là trọng tâm tam giác, N là các điểm được xác định bởi \(\overrightarrow{CN}\)= \(\dfrac{1}{3}\overrightarrow{BC}\) .Hãy tính \(\overrightarrow{AC}\) theo \(\overrightarrow{AG}\) và \(\overrightarrow{AN}\)