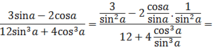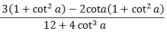biết tan a= 3 tính A=(sin3a- cos3a):(sin32+ cos3a)

Những câu hỏi liên quan
a. \(\dfrac{sina+sin3a+sin5a}{cosa+cos3a+cos5a}\)= tan3a
b. \(\dfrac{1+cosa}{1-cosa}tan^2\dfrac{a}{2}-cos^2a=sin^2a\)
giúp mk vs ạ
a.
\(\dfrac{sina+sin5a+sin3a}{cosa+cos5a+cos3a}=\dfrac{2sin3a.cosa+sin3a}{2cos3a.cosa+cos3a}=\dfrac{sin3a\left(2cosa+1\right)}{cos3a\left(2cosa+1\right)}=\dfrac{sin3a}{cos3a}=tan3a\)
b.
\(\dfrac{1+cosa}{1-cosa}.\dfrac{sin^2\dfrac{a}{2}}{cos^2\dfrac{a}{1}}-cos^2a=\dfrac{1+cosa}{1-cosa}.\dfrac{\dfrac{1-cosa}{2}}{\dfrac{1+cosa}{2}}-cos^2a\)
\(=\dfrac{1+cosa}{1-cosa}.\dfrac{1-cosa}{1+cosa}-cos^2a=1-cos^2a=sin^2a\)
Đúng 0
Bình luận (0)
Rút gọn A=\(\dfrac{\sin a+\sin3a+\sin5a}{\cos a+\cos3a+\cos5a}\)
A = \(\dfrac{2\sin3a.\cos2a+\sin3a}{2\cos3a.\cos2a+\cos3a}=\dfrac{\sin3a.\left(2\cos2a+1\right)}{\cos3a.\left(2\cos2a+1\right)} =\dfrac{\sin3a}{\cos3a}=\tan3a\)
Đúng 0
Bình luận (0)
Cho cota 3. Khi đó
3
sin
a
-
2
c
o
s
a
12
sin
3
a
+
4
cos
3...
Đọc tiếp
Cho cota = 3. Khi đó 3 sin a - 2 c o s a 12 sin 3 a + 4 cos 3 a có giá trị bằng
A. - 1 4
B. - 5 4
C. 3 4
D. 1 4
Chứng minh :
\(\frac{sina-sin3a-sin5a-sin7a}{cosa-cos3a-cos5a-cos7a}=-tan2a\)
Đề sai rồi bạn ơi, mình không biết các loại máy khác bấm như nào nhma mình dùng fx 580 thì mode B xét đúng/sai thì máy cho kết quả là biểu thức này sai nha :v
Đúng 0
Bình luận (0)
Don gian bieu thuc sau
a) A= \(\dfrac{1-cosa+cos2a}{sin2a-sina}\) b) B= \(\sqrt{\dfrac{1}{2}-\dfrac{1}{2}\sqrt{\dfrac{1}{2}+\dfrac{1}{2}cosa}}\) (0<a≤\(\pi\)).
c) C= \(\dfrac{cosa-cos3a+cos5a-cos7a}{sina+sin3a+sin5a+sin7a}\)
có A=\(\dfrac{1-cosa+2cos^2a-1}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)
Đúng 2
Bình luận (0)
rút gọn:
a, A=\(\frac{sina+sin2a+sin3a}{cosa+cos2a+cos3a}\)
b, B=\(\frac{sin^2a+sin^2a.tan^2a}{cos^2a+cos^2a.cot^2a}\)
\(A=\frac{sina+sin3a+sin2a}{cosa+cos3a+cos2a}=\frac{2sin2a.cosa+sin2a}{2cos2a.cosa+cos2a}=\frac{sin2a\left(2cosa+1\right)}{cos2a\left(2cosa+1\right)}=\frac{sin2a}{cos2a}=tan2a\)
\(B=\frac{sin^2a\left(1+tan^2a\right)}{cos^2a\left(1+cot^2a\right)}=\frac{sin^2a.\frac{1}{cos^2a}}{cos^2a.\frac{1}{sin^2a}}=\frac{sin^4a}{cos^4a}=tan^4a\)
Đúng 0
Bình luận (0)
Chứng minh các hệ thức sau :
a) \(\dfrac{1-2\sin^2a}{1+\sin2a}=\dfrac{1-\tan a}{1+\tan a}\)
b) \(\dfrac{\sin a+\sin3a+\sin5a}{\cos a+\cos3a+\cos5a}=\tan3a\)
c) \(\dfrac{\sin^4a-\cos^4a+\cos^2a}{2\left(1-\cos a\right)}=\cos^2\dfrac{a}{2}\)
d) \(\dfrac{\tan2x.\tan x}{\tan2x-\tan x}=\sin2x\)
c1 : chứng minh \(\left(\frac{1}{cos2x}+1\right)tanx=tan2x\)
c2 : chứng minh \(\frac{cos7a+cos5a+cos3a+cosa}{sin7a+sin5a+sin3a+sina}=cot4a\)
\(\left(\frac{1}{cos2x}+1\right)tanx=\left(\frac{cos2x+1}{cos2x}\right).\frac{sinx}{cosx}=\frac{2cos^2x}{cos2x}.\frac{sinx}{cosx}\)
\(=\frac{2sinx.cosx}{cos2x}=\frac{sin2x}{cos2x}=tan2x\)
\(\frac{cos7a+cosa+cos5a+cos3a}{sin7a+sina+sin5a+sin3a}=\frac{2cos4a.cos3a+2cos4a.cosa}{2sin4a.cos3a+2sin4a.cosa}\)
\(=\frac{cos4a\left(2cos3a+2cosa\right)}{sin4a\left(2cos3a+2cosa\right)}=\frac{cos4a}{sin4a}=cot4a\)
Đúng 0
Bình luận (0)
Giải bài này hộ em đi em giải quài không ra kết quả như đề
Chứng minh: Sina - sin3a - sin5a - sin7a / cosa - cos3a - cos5a - cos7a = - tan2a
Đơn giản vì đề bài không đúng, bạn thay thử 1 giá trị góc a vào và bấm máy sẽ thấy 2 vế ko hề bằng nhau
Đúng 0
Bình luận (0)
Biết 2\(Cos3a+Cos5a+Cosa=mCos^na.Cos3a\) . Tính m + n .
VT=cos3a+cos5a+cosa+cos3a
=2*cos4a*cosa+2*cosa*cos2a
=2*cosa*(cos4a+cos2a)
=2*cosa*2*(cos3a*cosa)
=4*cos3a*cos^2a
=>m=4; n=2
=>m+n=6
Đúng 0
Bình luận (0)