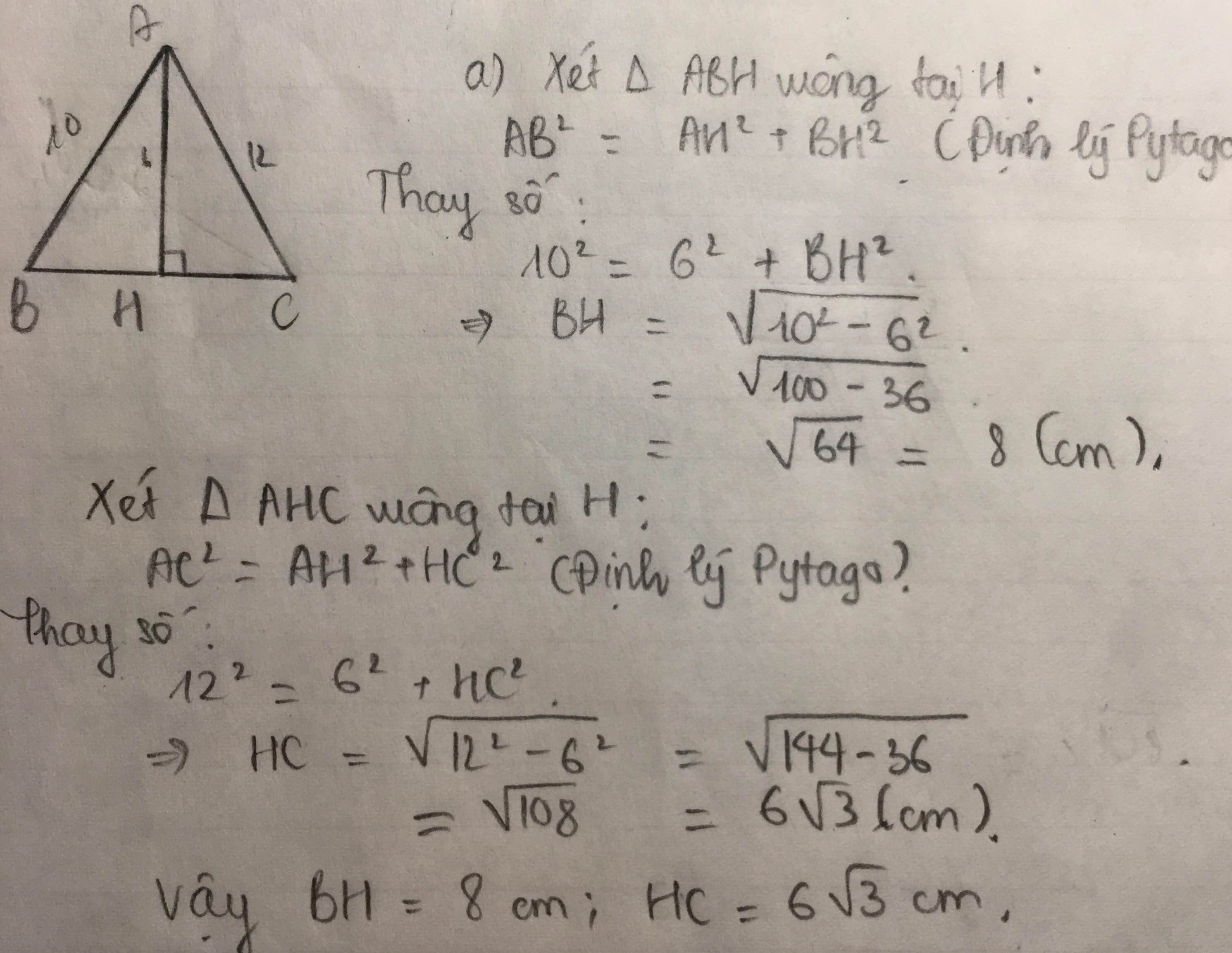Cho tam giác ABC vuông ở C. góc B = 30 độ, đường cao CH = 8 cm. Tính BH, BC, BA, CA

Những câu hỏi liên quan
1. Tam giác ABC vuông góc tại A, đường cao AH. Biết AB:AC3:4. Và AB+AC21a. Tính độ dài các cạnh tam giác ABCb. Tính độ dài các đoạn AH, BH, CH2. Cho hình thang ABCD có góc Agóc D 90 độ; góc B 60 độ; CD30 cm; CA vuông góc với CB. Tính diện tích hình thang1. Tam giác ABC vuông góc tại A, đường cao AH. Biết AB:AC3:4. Và AB+AC21a. Tính độ dài các cạnh tam giác ABCb. Tính độ dài các đoạn AH, BH, CH2. Cho hình thang ABCD có góc Agóc D 90 độ; góc B 60 độ; CD30 cm; CA vuông góc với CB. Tính diện tích hì...
Đọc tiếp
1. Tam giác ABC vuông góc tại A, đường cao AH. Biết AB:AC=3:4. Và AB+AC=21
a. Tính độ dài các cạnh tam giác ABC
b. Tính độ dài các đoạn AH, BH, CH
2. Cho hình thang ABCD có góc A=góc D= 90 độ; góc B= 60 độ; CD=30 cm; CA vuông góc với CB. Tính diện tích hình thang
1. Tam giác ABC vuông góc tại A, đường cao AH. Biết AB:AC=3:4. Và AB+AC=21
a. Tính độ dài các cạnh tam giác ABC
b. Tính độ dài các đoạn AH, BH, CH
2. Cho hình thang ABCD có góc A=góc D= 90 độ; góc B= 60 độ; CD=30 cm; CA vuông góc với CB. Tính diện tích hình thang
AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm
Đúng 0
Bình luận (0)
Cho tam giác ABC, vuông ở A , có góc B = 30 độ , vẽ tia phân giác CD , D thuộc AB , trên tia BC lấy điểm M sao CA =CM
a) Cm : Góc DBC = gócACD
b) CM : DA =DM
c) Qua B kẻ BM vuông góc với đường thẳng CD , BH vuông BC . CM BH = BM
b: Xét ΔDCA và ΔDCM có
DC chung
\(\widehat{DCA}=\widehat{DCM}\)
CA=CM
Do đó: ΔDCA=ΔDCM
Suy ra: DA=DM
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A có AB = 6 cm AC = 8 cm Vẽ đường cao AH AC tính BC b Chứng minh tam giác ABC đồng dạng tam giác ahb c a chứng minh AB vuông bằng BH nhân BC nhân tính bh , b c đi Vẽ phân giác AD của góc A D thuộc BC Tính dB
a: BC=căn 6^2+8^2=10cm
b: Xét ΔBAC vuông tại A và ΔBHA vuông tại H có
góc B chung
=>ΔBAC đồng dạng với ΔBHA
c: BA/BH=BC/BA
=>BA^2=BH*BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 3 cm AC = 4 cm , đường cao AH a, CM : tam giác ABC đồng dạng tam giác HBA từ đó suy ra ab² = BC . BH b , tính BC và BH c, Kẻ HE vuông góc AB , HF vuông góc AC Chứng minh AH . BH = BE.AC và tính độ dài BE
a: Xet ΔABC vuông tại A và ΔHBA vuông tại H co
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A và AB=6 , AC=8 , đường cao AH. Tia phân giác của góc BAH cắt BH tại D.Trên tia CA lấy k sao cho Ck=BC.
a, cmr:BK//AD
b cm KD vuông góc BC
c Tính KB
1. Tam giác ABC vuông góc tại A, đường cao AH. Biết AB:AC=3:4. Và AB+AC=21
a. Tính độ dài các cạnh tam giác ABC
b. Tính độ dài các đoạn AH, BH, CH
2. Cho hình thang ABCD có góc A=góc D= 90 độ; góc B= 60 độ; CD=30 cm; CA vuông góc với CB. Tính diện tích hình thang
Bài 1:
a: \(AB=21\cdot\dfrac{3}{7}=9\left(cm\right)\)
AC=21-9=12(cm)
=>BC=15(cm)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=7,2(cm)
Xét ΔAHB vuông tại H có \(AB^2=AH^2+BH^2\)
hay BH=5,4(cm)
=>CH=9,6(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A, đường cao AH, biết BH = 4 cm, CH = 9 cm. Hãy tính ( kết quả về độ dài là tròn đến chữ số thập phân thứ ba, số đo góc làm tròn đến độ):
a. Dộ dài cạnh AB và đường cao AH.
b. Góc B rồi từ đó tính độ dài cạnh AC.
c. Diện tích tam giác ABC.
cho tam giác ABC cân tại C .Kẻ AH vuông góc vs BC (H thuộc BC ).Cho AH =6 cm ,AB =10 cm ,AC =12 cm
a)Tính BH và CH
b) tính độ dài đường cao hạ từ C xuống AB
Cho tam giác ABC cân tại C .Kẻ AH vuông góc với BC (H thuộc BC ) Cho AH =6cm ,AB =10 cm ,AC =12 cm a)Tính BH ,CH b)Tính độ dài đường cao hạ từ C xuống AB