so sánh a/b và a+1/b+1 Trường hợp a/b >1

Những câu hỏi liên quan
so sánh a/b với a+1/b+1
a,Trường hợp a/b>1
b,Trường hợp a/b<1
So sánh hai số a và b trong mỗi trường hợp sau:
a) a, b là hai số dương và |a| < |b|;
b) a, b là hai số âm và |a| < |b|
a) Khi a, b là hai số dương:
|a| = a; |b| = b
Khi đó, |a| < |b| , tức là a < b
Vậy a < b
b) Khi a, b là hai số âm:
|a| = - a; |b| = - b
Khi đó, |a| < |b| , tức là - a < - b hay a > b
Vậy a > b
Đúng 1
Bình luận (0)
a: |a|<|b|
mà a,b dương
nên a<b
b: a,b là hai số âm
|a|<|b|
Do đó: a>b
Đúng 0
Bình luận (0)
Ai giải giùm bài này với
Cho phân số a/b, cộng cả tử số và mẫu số của phân số trên với số tự nhiên m khác 0 ta được 1 phân số mới. Hãy so sánh phân số a/b với phân số mới nhận được bằng cách trên.
( Gợi ý: xét 2 trường hợp a/b < 1 và a/b > 1
Bài 1 Tìm hai phân số khác nhau,các phấn số này lớn hơn 1/5 nhưng nhỏ hơn 1/4.Bài 2 : a) Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b 1 và m thuộc tập hợp N,m khác 0 . Chứng tỏ rằng a/ba+m/b+mb) Áp dụng kết quả ở câu a) để só sánh 434/561 và 441/568Bài 3 : Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b 1 và m thuộc tập hợp N,m khác 0.Chứng tỏ rằng a/ba+m/b+mb) Áp dụng kết quả ở câu a) để só sánh: 237/142 và 246/151Bài 4: So sánh : A1718+1/1719+1 và B 1717+1/1718+1B...
Đọc tiếp
Bài 1 Tìm hai phân số khác nhau,các phấn số này lớn hơn 1/5 nhưng nhỏ hơn 1/4.
Bài 2 : a) Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b < 1 và m thuộc tập hợp N,m khác 0 . Chứng tỏ rằng
a/b<a+m/b+m
b) Áp dụng kết quả ở câu a) để só sánh 434/561 và 441/568
Bài 3 : Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b > 1 và m thuộc tập hợp N,m khác 0.Chứng tỏ rằng
a/b>a+m/b+m
b) Áp dụng kết quả ở câu a) để só sánh: 237/142 và 246/151
Bài 4: So sánh : A=1718+1/1719+1 và B = 1717+1/1718+1
Bài 5 : So sánh : C=9899+1/9889+1 và D = 9898+1/9888+1
Cho a,b,n thuộc Z; b,n0.a) Chứng minh: dfrac{a}{b}1Leftrightarrow ab và dfrac{a}{b} 1Leftrightarrow a bb) So sánh 2 số hữu tỉ dfrac{a}{b} và dfrac{a+1}{b+1}c) So sánh dfrac{a}{b} và dfrac{a+n}{a+n}
Đọc tiếp
Cho a,b,n thuộc Z; b,n>0.
a) Chứng minh: \(\dfrac{a}{b}>1\Leftrightarrow a>b\) và \(\dfrac{a}{b}< 1\Leftrightarrow a< b\)
b) So sánh 2 số hữu tỉ \(\dfrac{a}{b}\) và \(\dfrac{a+1}{b+1}\)
c) So sánh \(\dfrac{a}{b}\) và \(\dfrac{a+n}{a+n}\)
\(a,\dfrac{a}{b}>1\Leftrightarrow a>1\cdot b=b\\ \dfrac{a}{b}< 1\Leftrightarrow a< 1\cdot b=b\\ b,\dfrac{a}{b}=\dfrac{a\left(b+1\right)}{b\left(b+1\right)}=\dfrac{ab+a}{b^2+b}\\ \dfrac{a+1}{b+1}=\dfrac{b\left(a+1\right)}{b\left(b+1\right)}=\dfrac{ab+b}{b^2+b}\\ \forall a=b\Leftrightarrow\dfrac{a}{b}=\dfrac{a+1}{b+1}\\ \forall a>b\Leftrightarrow\dfrac{a}{b}>\dfrac{a+1}{b+1}\\ \forall a< b\Leftrightarrow\dfrac{a}{b}< \dfrac{a+1}{b+1}\)
\(c,\forall a>b\Leftrightarrow\dfrac{a}{b}-1=\dfrac{a-b}{b}>\dfrac{a-b}{b+n}\left(b< b+n;a-b>0\right)=\dfrac{a+n}{b+n}-1\\ \Leftrightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\\ \forall a< b\Leftrightarrow1-\dfrac{a}{b}=\dfrac{b-a}{b}>\dfrac{b-a}{b+n}\left(b< b+n;b-a>0\right)=1-\dfrac{a+n}{b+n}\\ \Leftrightarrow1-\dfrac{a}{b}>1-\dfrac{a+n}{b+n}\Leftrightarrow\dfrac{a}{b}>\dfrac{a+n}{b+n}\\ \forall a=b\Leftrightarrow\dfrac{a+n}{b+n}=\dfrac{a}{b}\left(=1\right)\)
Đúng 2
Bình luận (0)
a) Tính giá trị biểu thức sau:
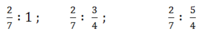
b) So sánh số chia với 1 trong mỗi trường hợp.
c) So sánh giá trị tìm được với số bị chia rồi rút ra kết luận.
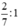 |
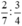 |
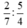 |
|
| a) Tính: | 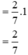 |
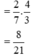 |
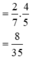 |
| b) So sánh số chia với 1. |
1 = 1 | 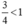 |
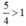 |
| c) So sánh thương với số bị chia. |
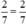 |
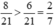 |
Kết luận:
- Một phân số chia cho 1 bằng chính nó.
- Một phân số chia cho phân số nhỏ hơn 1 sẽ lớn hơn chính nó.
- Một phân số chia cho phân số lớn hơn 1 sẽ nhỏ hơn chính nó.
Đúng 0
Bình luận (0)
a, Cho a,b,n ϵ N* . Hãy so sánh dfrac{a+n}{b+n}vàdfrac{a}{b}b, Cho A dfrac{10^{11}-1}{10^{12}-1};Bdfrac{10^{10}+1}{10^{11}+1}. So sánh A và B
Đọc tiếp
a, Cho a,b,n ϵ N* . Hãy so sánh \(\dfrac{a+n}{b+n}và\dfrac{a}{b}\)
b, Cho A= \(\dfrac{10^{11}-1}{10^{12}-1};B=\dfrac{10^{10}+1}{10^{11}+1}.\) So sánh A và B
Lời giải:
a) Xét hiệu \(\frac{a+n}{b+n}-\frac{a}{b}=\frac{(a+n).b-a(b+n)}{b(b+n)}=\frac{n(b-a)}{b(b+n)}\)
Nếu $b>a$ thì $\frac{a+n}{b+n}-\frac{a}{b}>0\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$
Nếu $b<a$ thì $\frac{a+n}{b+n}-\frac{a}{b}<0\Rightarrow \frac{a+n}{b+n}<\frac{a}{b}$
Nếu $b=a$ thì $\frac{a+n}{b+n}-\frac{a}{b}=0\Rightarrow \frac{a+n}{b+n}=\frac{a}{b}$
b) Rõ ràng $10^{11}-1< 10^{12}-1$.
Đặt $10^{11}-1=a; 10^{12}-1=b; 11=n$ thì: $a< b$; $A=\frac{a}{b}$ và $B=\frac{10^{11}+10}{10^{12}+10}=\frac{a+n}{b+n}$
Áp dụng kết quả phần a:
$b>a\Rightarrow \frac{a+n}{b+n}>\frac{a}{b}$ hay $B>A$
Đúng 2
Bình luận (2)
1 ) so sánh : A= 3450 và B= 5300
2) tìm các số tự nhiên x ,y trong mỗi trường hợp sau đây
Lộn, lộn,
\(3^{450}=\left(3^3\right)^{150}=27^{150}\)
Vì \(27^{150}>25^{150}\)nên \(A>B\)
Đúng 0
Bình luận (0)
1) Ta có: \(3^{450}=\left(3^3\right)^{150}=9^{150}\).
\(5^{300}=\left(5^2\right)^{150}=25^{150}\)
Ví \(9^{150}< 25^{150}\)nên \(3^{450}< 5^{300}\)
\(\Rightarrow A< B\)
Đúng 0
Bình luận (0)
So sánh A=\(\dfrac{1}{100}+\dfrac{1}{101}+\dfrac{1}{102}+..+\dfrac{1}{2021}\)và B=20. So sánh A và B




















