c/m
a,-x2+16x-41<0
b,(x-3)(x-5)+4>0
Không thực hiện phép tính , hãy tìm các cặp kết quả bằng nhau trong các kết quả sau :
a = 42 - (321- 410)
b = 42 - 410 - 321
c = 42 - 410 + 321
d, 42 - (321 + 410 )
e, 42 + 410 - 321
a=42-321+410=e
b=42-410-321=d
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3 x 2 − 8 x 3
b) y = 16x + 2 x 2 − 16 x 3 /3 − x 4
c) y = x 3 − 6 x 2 + 9x
d) y = x 4 + 8 x 2 + 5
a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 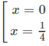
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 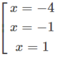
Bảng biến thiên:
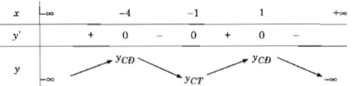
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 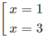
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)
Phân tích đa thức thành nhân tử:
a) 2 x 3 - x 2 - 8x + 4; b) 4 x 2 - 16 x 2 y 2 + y 2 + 4xy;
c) x 3 - 16x - 15x(x - 4); d) x ( x - y ) 2 + y ( x - y ) 2 - xy + x 2 .
Điền vào...
a)x2+12x+...=(....)2
b)x2+81+...=(....)2
c)x2-16x+...=(....)2
d)16-2x+...=(....)2
a)x2 + 12x + 36 =(x + 6)2
2 + 81 + 18x =(x + 9)2
2- 16x + 64 =(x - 8)2
2
a)x2+12x+.36..=(..x+6..)2
b)x2+81+.18x..=(..x+9..)2
c)x2-16x+.64..=(..x-8..)2
d)16-2x+...=(....)2
Câu cuối có bị lỗi không nhỉ ?
\(a,...+....36=\left(x-6\right)^2\)
\(b,....+1640,25=\left(x+40,5\right)^2\)
\(c,....+64=\left(x-8\right)^2\)
\(d,...+\left(\dfrac{1}{16}x\right)^2=\left(4-\dfrac{1}{4}x\right)^2\)
Tìm tâm và bán kính của các đường tròn sau:
a, x2 + y2– 2x – 2y - 2 = 0
b, 16x2 + 16y2 + 16x – 8y -11 = 0
c, x2 + y2 - 4x + 6y – 3 = 0
Cách 1 : Xác định các hệ số a, b, c.
a) x2 + y2 – 2x – 2y – 2 = 0 có hệ số a = 1 ; b = 1 ; c = –2
⇒ tâm I (1; 1) và bán kính 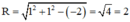
b) 16x2 + 16y2 + 16x – 8y –11 = 0
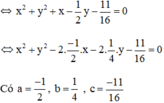
⇒ Đường tròn có tâm 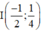 , bán kính
, bán kính 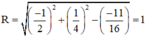
c) x2 + y2 - 4x + 6y - 3 = 0
⇔ x2 + y2 - 2.2x - 2.(-3).y - 3 = 0
có hệ số a = 2, b = -3,c = -3
⇒ Đường tròn có tâm I(2 ; –3), bán kính 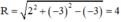
Cách 2 : Đưa về phương trình chính tắc :
a) x2 + y2 - 2x - 2y - 2 = 0
⇔ (x2 - 2x + 1) + (y2 - 2y +1) = 4
⇔(x-1)2 + (y-1)2 = 4
Vậy đường tròn có tâm I(1 ; 1) và bán kính R = 2.
b) 16x2 + 16y2 + 16x - 8y - 11 = 0
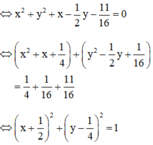
Vậy đường tròn có tâm 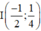 và bán kính R = 1.
và bán kính R = 1.
c) x2 + y2 - 4x + 6y -3 = 0
⇔ (x2 - 4x + 4) + (y2 + 6y + 9) = 4 + 9 + 3
⇔ (x - 2)2 + (y + 3)2 = 16
Vậy đường tròn có tâm I( 2 ; –3) và bán kính R = 4.
không thực hiện phép tính, hãy tìm các cặp kết quả bằng nhau trong các kết quả sau:
a=42-(321-410)
b=42-410-321
c=42-410+321
n=42+421-321
m=42-(321+410)
Phân tích các đa thức sau thành nhân tử:
a) a/ x3 – 2x2 + x – xy2
b) 4x2 + 16x + 16
c) (x2 + x)2 + 4(x2+ x) - 12
Bạn ơi mk làm 3 phần a,b,c rồi đấy, bạn vào xem đi
Chúc bạn học tốt!
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x = x 2 - 16 x trên đoạn - 4 ; 1 . Tính T = M + m
A. T = 32
B. T = 16
C. T = 37
D. T = 25
Hàm số f x = x 2 − 16 x − 2 k h i x > 4 3 x − m k h i x ≤ 4 liên tục tại x 0 = 4 khi m nhận giá trị là
A. 44
B. -20
C. 20
D. m bất kỳ
Đáp án B
Ta có: lim x → 4 − f x = lim x → 4 − 3 x − m = 12 − m
lim x → 4 + f x = lim x → 4 + x 2 − 16 x − 2 = lim x → 4 + x − 4 x + 4 x + 2 x − 4 = lim x → 4 + x + 4 x + 2 = 32
Để hàm số liên tục tại x = 4 thì lim x → 4 − f x = lim x → 4 + f x = f 4 ⇔ 12 − m = 32 ⇔ m = − 10
x2 - 16x - y2 + 64 =?
x2 - 7x + 7y - y2 = ?
x2 - 16x - y2 + 64 = (x−8+y)(x−8−y)
x2 - 7x + 7y - y2 = (x-y)(x+y-7)