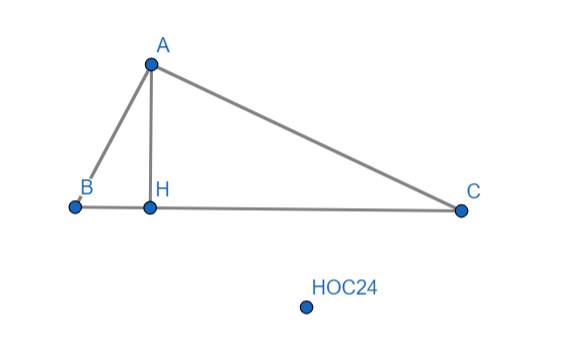
Cho tam giác ABC, Â=900 , đường cao AH biết

Những câu hỏi liên quan
1 Giải tam giác vuông ABC biết rằng  900 và :a) b 10 cm, ; b) c 10 cm, ; c) a 20 cm, ; d) c 21 cm, b 18 cm; 2 Cho DABC nhọn có đường cao AH và đường trung tuyến AM. Biết , AB 9 cm, AC 12 cm. Giải tam giác ABC và tính AM.
Đọc tiếp
1 Giải tam giác vuông ABC biết rằng  = 900 và :
a) b = 10 cm, ; b) c = 10 cm, ;
c) a = 20 cm, ; d) c = 21 cm, b = 18 cm;
2 Cho DABC nhọn có đường cao AH và đường trung tuyến AM. Biết , AB = 9 cm, AC = 12 cm. Giải tam giác ABC và tính AM.
Bài 1:
d) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+18^2=765\)
hay \(BC=3\sqrt{85}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{21}{3\sqrt{85}}\)
nên \(\widehat{C}\simeq49^023'\)
\(\Leftrightarrow\widehat{B}=40^037'\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông (Â=90) đường cao AH. Biết AB:AC =3:4 và BC =15cm. Tính BH và CH.?
BA/AC=3/4
nên HB/HC=(3/4)^2=9/16
=>HB/9=HC/16=(HB+HC)/(9+16)=15/25=0,6
=>HB=5,4cm; HC=9,6cm
Đúng 0
Bình luận (0)
Cho tam giác ABC, Â=90 , đường cao AH biết AH.AC=3.5 và AB=15cm.
a/ Tính HB, HC
b/ Gọi E, F là hình chiếu của H lên AB,AC c/m AH^3 = BC.BE.CF
Để giải bài toán, ta sẽ sử dụng các định lý trong hình học tam giác. a/ Để tính HB và HC, ta cần tìm độ dài đường cao AH trước. Với thông tin AH.AC = 3.5 và AC = 15cm, ta có thể tính được AH: AH = (AH.AC)/AC = (3.5)/(15) = 0.2333 cm Tiếp theo, ta xét tam giác ABC với tam giác ABC. góc B và đường cao AH. Áp dụng định lý Pythagoras, ta có công thức: AB^2 = AH^2 + BH^2 Với độ dài AB = 15cm, ta có: 15^2 = 0,2333^2 + BH^2 225 = 0,0544 + BH^2 BH^2 = 224,9456 BH ≈ 14,998 cm Tương tự, ta có: HC ≈ 0,2333 cm Vậy HB ≈ 14,998 cm và HC ≈ 0,2333 cm. b/ Để chứng minh AH^3 = BC.BE.CF, ta sẽ sử dụng các tỷ lệ trong tam giác tương đồng. Kiểm định tam giác AHB và tam giác AFC, ta có: AH/AF = HB/FC 0.2333/AF = 14.998/(15 - FC) Tương tự, xét tam giác AHC và tam giác AEB, ta có: AH/AE = HC/EB 0.2333/AE = 0.2333/(15 - EB ) Từ hai tỷ lệ trên, ta có: AF/(15 - FC) = AE/(15 - EB) Nhân cả hai quan sát với (15 - FC)(15 - EB), ta có: AF(15 - EB) = AE(15 - FC) Vậy ta có BC.BE.CF = AF(15 - EB) = AE(15 - FC) = AH^2. Do đó, AH^3 = BC.BE.CF.
Đúng 0
Bình luận (0)
a: Sửa đề: AH/AC=3/5
Xét ΔAHC vuông tại H có sin C=AH/AC=3/5
Xét ΔABC vuông tại A có sin C=AB/BC
=>15/BC=3/5
=>BC=25(cm)
=>\(AC=\sqrt{25^2-15^2}=20\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2; CH*CB=CA^2
=>BH=15^2/25=9cm; CH=20^2/25=16cm
b: BC*BE*CF
=BC*BH^2/BA*CH^2/CA
=AH^4/AH
=AH^3
Đúng 0
Bình luận (0)
Cho tam giác ABC, Â=90 , đường cao AH biết AH.AC=3.5 và AB=15cm.
a/ Tính HB, HC
b/ Gọi E, F là hình chiếu của H lên AB,AC c/m AH^3 = BC.BE.CF
Đề đúng là: \(\dfrac{AH}{AC}=\dfrac{3}{5}\). Bạn tự vẽ hình nhé.
(a) Theo đề: \(\dfrac{AH}{AC}=\dfrac{3}{5}\Leftrightarrow AC=\dfrac{5}{3}AH\)
Ta có: \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Leftrightarrow BC^2=15^2+\left(\dfrac{5}{3}AH\right)^2\Rightarrow BC=\sqrt{225+\dfrac{25}{9}AH^2}\)
Lại có: \(AB^2=BC.HB\Leftrightarrow HB=\dfrac{AB^2}{BC}=\dfrac{15^2}{\sqrt{225+\dfrac{25}{9}AH^2}}\)
Ta cũng có: \(AH^2=HB.HC=HB\left(BC-HB\right)=BC.HB-HB^2\)
\(\Leftrightarrow AH^2=\sqrt{225+\dfrac{25}{9}AH^2}\cdot\dfrac{15^2}{\sqrt{225+\dfrac{25}{9}AH^2}}-\left(\dfrac{15^2}{\sqrt{225+\dfrac{25}{9}AH^2}}\right)^2\)
\(=15^2-\dfrac{15^4}{225+\dfrac{25}{9}AH^2}\)
\(\Rightarrow AH=12\left(cm\right)\)
Thay vào tính được: \(HB=9\left(cm\right);BC=25\left(cm\right)\)
\(\Rightarrow HC=BC-HB=25-9=16\left(cm\right)\)
(b) Xét \(\Delta AHB\) vuông tại \(H:BE.AB=HB^2\Leftrightarrow BE=\dfrac{HB^2}{AB}\)
Tương tự, \(\Delta AHC\) vuông tại \(H:CF.AC=HC^2\Leftrightarrow CF=\dfrac{HC^2}{AC}\)
Ta có: \(BC.BE.CF=\left(\dfrac{AB.AC}{AH}\right)\cdot\dfrac{HB^2}{AB}\cdot\dfrac{HC^2}{AC}\)
\(=\dfrac{HB^2.HC^2}{AH}=\dfrac{\left(HB.HC\right)^2}{AH}=\dfrac{\left(AH^2\right)^2}{AH}=AH^3\left(đpcm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC ( ∠ A = 90 0 ) có đường cao AH. Chứng minh rằng A H 2 = B H . C H
Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: 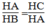
Vậy A H 2 = B H . C H
Đúng 0
Bình luận (0)
Tam giác vuông ABC (A = 90 0 ) có đường cao AH và trung tuyến AM. Tính diện tích tam giác AMH,biết rằng BH = 4cm, CH = 9cm
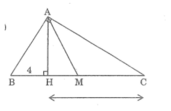
Xét hai tam giác vuông HBA,HAC có:
∠ (BHA) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ ∠ C )
⇒ △ HBA đồng dạng △ HAC (g.g)
Suy ra: 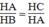
⇒ H A 2 = HB.HC = 4.9 = 36(cm)
Suy ra: AH = 6(cm)
Lại có: BM = 1/2 BC = 1/2 .(9+4) = 1/2 .13 = 6,5cm
Mà HM = BM – BH = 6,5 – 4 = 2,5cm
Vậy S A H M = 1/2 AH.HN = 1/2 .6.2,5 = 7,5 c m 2
Đúng 1
Bình luận (0)
: Cho tam giác ABC (Â 900); hạ AH ^ BC (H BC). Trên tia đối tia HA lấy điểm D sao cho HAHD.a) Chứng minh AB DB.b) Chứng minh c) Chứng minh AC2 + HB2 AB2 + HC2d) Qua A kẻ đường thẳng song song với BD và cắt BC tại E. Biết 2 . Tam giác ABE là tam giác gì. Vì sao ? mong mn giúp mình nhanh nhất có thể
Đọc tiếp
: Cho tam giác ABC (Â = 900); hạ AH ^ BC (H BC). Trên tia đối tia HA lấy điểm D sao cho HA=HD.
a) Chứng minh AB = DB.
b) Chứng minh =
c) Chứng minh AC2 + HB2 = AB2 + HC2
d) Qua A kẻ đường thẳng song song với BD và cắt BC tại E. Biết = 2 . Tam giác ABE là tam giác gì. Vì sao ?
mong mn giúp mình nhanh nhất có thể
Cho tam giác ABC vuông tại A, Â=90, tan C=2/3, đường cao AH =6cm.Tính HB,HC,AB,AC?
ta có
tan C=\(\frac{AH}{CH}\)
=> CH=\(\frac{AH}{\tan C}\)
CH=\(\frac{6}{\frac{2}{3}}=6.\frac{3}{2}=9\left(cm\right)\)
Xét tam giác AHC vuông tại H:
AH2+HC2=AC2 (py - ta -go)
AC2=62+92
AC2=117
=>AC=\(3\sqrt{13}\)(cm)
tan C = \(\frac{AB}{AC}\)
=>AB= tan C .AC
AB=\(\frac{2}{3}.3\sqrt{13}=2\sqrt{13}\)(cm)
Xét tam giác ABC vuông tại A:
AB2+AC2=BC2
\(\left(3\sqrt{13}\right)^2+\left(2\sqrt{13}\right)^2=BC^2\)
BC2=169
=>BC=13 (cm)
Đúng 0
Bình luận (0)
cho tam giác abc (Â=90độ).
có độ cao AH biết HB=4CM HC=9CM
A)tính ab,ah,ac
B) tính diện tích tam giác abc
Giúp mik vs ạ mik mong rằng sẽ có bn nào giúp
Xét \(\Delta ABC\) và \(\Delta HBA\) có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
\(\widehat{B}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\) (1)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{HB}{AB}\) hay \(\dfrac{AB}{4+9}=\dfrac{4}{AB}\Rightarrow AB^2=52\Rightarrow AB=\sqrt{52}=2\sqrt{13}cm\)
Xét \(\Delta\text{A}BC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{C}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g.g\right)\) (2)
Từ (1) và (2) \(\Rightarrow\Delta HAB\sim\Delta HCA\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{HB}{AH}\) hay \(\dfrac{AH}{9}=\dfrac{4}{AH}\Rightarrow AH^2=36\Rightarrow AH=\sqrt{36}=6\left(cm\right)\)
Ta có \(\Delta ABC\) vuông tại A.
Áp dụng đinh lý Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{\left(4+9\right)^2-\left(2\sqrt{13}\right)^2}=3\sqrt{13}cm\)
b) Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot AH=\dfrac{1}{2}\cdot\left(4+9\right)\cdot6=39\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC có góc B và góc C nhỏ hơn 900 . Vẽ ra phía ngoài tam giác ấy các tam giác vuông cân ABD và ACE ( trong đó góc ABD và góc ACE đều bằng 900 ), vẽ DI và EK cùng vuông góc với đường thẳng BC. AH là đường cao của tam giác ABC. Chứng minh rằng: a. BI=AH; EK = HC; b. BC = DI + EK.: