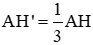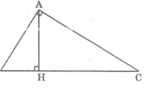
Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: 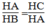
Vậy A H 2 = B H . C H

Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: 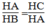
Vậy A H 2 = B H . C H
C1. Cho tam giác nhọn DEF. Đường cao EA và FB cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C2. Cho tam giác nhọn ABC. Đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C3. Cho ABC vuông tại A, đư¬ờng cao AH cắt đ¬ường phân giác CD tại I.
a) Chứng minh rằng:
b) Chứng minh AC2 = CH.BC
C4. Cho hình bình hành ABCD, trên cạnh AB lấy một điểm M. Đường thẳng DM cắt cạnh CB kéo dài tại N.
a) Chứng minh : MAD MBN
b) Chứng minh : MA.MN = MD.MB
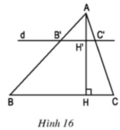
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H' (h.16).
a) Chứng minh rằng: A H ' A H = B ' C B C
b) Áp dụng: Cho biết A H ' A H = 1 3 và diện tích tam giác ABC là 67,5 cm2. Tính diện tích tam giác AB’C’.
Cho tam giác ABC vuông tại A, AB<AC, có AH là đường cao(H thuộc BC). Chứng minh rằng:
a) Tam giác HBA đồng dạng tam giác ABC và HB*AC= HA*AB
b) HA^2=hb*HC
c) Gọi M là trung điểm AH. Trên tia đối tia AC lấy N sao cho AN=1/2AC. Chứng minh: tam giác BHM đồng dạng tam giác BAN
d) Góc BMN=90 độ
cho tam giác abc có góc a=90 độ, ab=6cm, ac=8cm. vẽ đường cao ah. a) tính bc b) chứng minh ab^2= bh.bc. tính bh, hc c) vẽ phân giác ad của góc a ( d thuộc bc ). chứng minh h nằm giữa b và d
cho tam giác abc nhọn có hai đường cao bd và ce .a) chứng minh tam giác abd đồng dạng với tam ace , b)chứng minh tam giác adeđồng dạng với tam giác abc ,c) gọi h là giao điểm của bdvà ce,k là giao điểm của ah và bc . chứng minh rằng : ah vuông góc với bc và chnhân vớice bằng bc nhân với ck
Cho tam giác vuông ABC ( góc A = 90 độ), đường cao AH (H thuộc BC).
a, Chứng minh rằng : AB^2 = HB . HC
b, Gọi D, E lần lượt là hình chiếu của H trên AB, AC. Chứng minh : AD.BE=AE.AC
c, Gọi i là trung điểm của EH. Tia AI cắt BC tại M. Chứng minh: EH là tia phân giác của góc BEM
Cho tam giác ABC vuông tại A, đường trung tuy n AM, đường cao AH. Gọi D, E theo thứ
tự là chân đường vuông góc kẻ t H n AB, AC. Chứng minh rằng
a) AH = DE b) H ̂ B = M ̂ C
c) AM vuông góc DE
d) Chứng minh DICE là hình thang biết I l trung điểm của HB v K l trung điểm của HC
Cho tam giác ABC vuông tại A có AH là đường cao. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.
a) Chứng minh ADHE là hình chữ nhật
b) Chứng minh tam giác AED đồng dạng tam giác ABC
c) Cho biết diện tính ABC= 2 diện tích ADHE. Chứng minh rằng tam giác ABC vuông cân tại A
cho tam giác abc có góc a=90 độ, ab=6cm, ac=8cm. vẽ đường cao ah.
a) tính bc
b) chứng minh ab^2= bh.bc. tính bh, hc
c) vẽ phân giác ad của góc a ( d thuộc bc ). chứng minh h nằm giữa b và d
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H'
a) Chứng minh rằng: 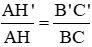
b) Áp dụng: Cho biết