a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒ 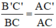
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒ 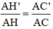
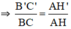
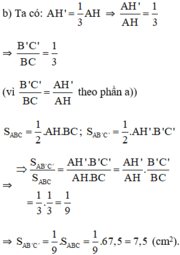
a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒ 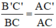
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒ 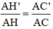
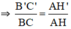
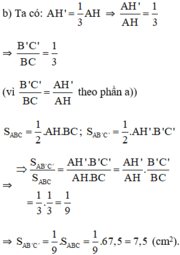
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC cắt các cạnh AB, AC và đường cao AH theo thứ tự tại các điểm B', C' và H'
a) Chứng minh rằng: 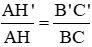
b) Áp dụng: Cho biết 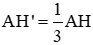
Tam giác ABC có đường cao AH . Đường thẳng d song song với BC , cắt các cạnh AB , AC và đường cao AH theo thứ tự tại các điểm B' , C' và H' .
a) CMR : AH'/AH = B'C'/BC .
b) Cho AH' = 1/3 AH và S tam giác ABC là 67,5 cm2 . Tính S tam giác AB'C' .
Cho tam giác ABC có đường cao AD. Đường thẳng song song với BC, cắt AB,AC và đường cao AD theo thứ tự tại các điểm B',C',D'
a) chứng minh AD'/AD=B'C'/BC
b) Áp dụng: Cho biết AD'=1/3AD và diện tích tam giác ABC là 73,5cm^2. Tính diện tích tam giác AB'C'
Cho tam giác ABC, đường cao AH, đường thẳng d song song bới BC cắt AB tại B', cắt AC tại C', cắt AH tại H'.
a) Chứng minh \(\frac{AH'}{AH}\)= \(\frac{B'C'}{BC}\)
b) Biết AH' = \(\frac{1}{3}\)AH, diện tích tam giác ABC bằng 67,5 cm2. Tính diện tích tam giác A'B'C'.
Cho tam giác ABC nhọn (AB<AC). các đường cao AE , BF cắt nhau tại H. gọi M là trung điểm của BC qua H vẽ đường thẳng a vuông góc với HM , a cắt AB , Ac lần lượt tại I và K. a) cm: Tam giác ABC ~ Tam giác EFC b) Qua C kẻ đường thẳng b song song với IK , b cắt AH, AB theo thứ tự tại N và D . cm : NC=ND và HI=HK c) Gọi G là giao điểm của CH và AB ,cm: AH/HE + BH/HF + CH/HG > 6
Cho tam giác ABC có BC = a. Đường cao AH = h. Từ 1 điểm M trên AH vẽ đường thẳng song song với BC cắt AB, AC lần lượt tại P, Q. Vẽ PS và QR vuông góc với BC.
a. Tính diện tích tứ giác theo a, h, x với x = AM.
b. Xác định M trên AH để diện tích tứ giác PQRS lớn nhất.
Cho tam giác ABC nhọn (AB<AC). các đường cao AE , BF cắt nhau tại H. gọi M là trung điểm của BC qua H vẽ đường thẳng a vuông góc với HM , a cắt AB , Ac lần lượt tại I và K.
a) cm: Tam giác ABC ~ Tam giác EFC
b) Qua C kẻ đường thẳng b song song với IK , b cắt AH, AB theo thứ tự tại N và D . cm : NC=ND và HI=HK
c) Gọi G là giao điểm của CH và AB ,cm:
AH/HE + BH/HF + CH/HG > 6
Cho tam giác ABC nhọn (AB<AC). các đường cao AE , BF cắt nhau tại H. gọi M là trung điểm của BC qua H vẽ đường thẳng a vuông góc với HM , a cắt AB , Ac lần lượt tại I và K.
a) cm: Tam giác ABC ~ Tam giác EFC
b) Qua C kẻ đường thẳng b song song với IK , b cắt AH, AB theo thứ tự tại N và D . cm : NC=ND và HI=HK
c) Gọi G là giao điểm của CH và AB ,cm:
AH/HE + BH/HF + CH/HG > 6