Cho tam giác ABC nhọn,đường tròn tâm O,đường kính BC cắt 2 cạnh AB,AC lần lượt tại M và N.Gọi H là giao điểm của BN và CM
a)Chứng minh AH vuông góc với BC
b) Chứng minh MN<BC
c)Gọi I là trung điểm MN.Chứng minh OI vuông góc với MN
Cho tam giác ABC nhọn,đường tròn tâm O,đường kính BC cắt 2 cạnh AB,AC lần lượt tại M và N.Gọi H là giao điểm của BN và CM
a)Chứng minh AH vuông góc với BC
b) Chứng minh MN<BC
c)Gọi I là trung điểm MN.Chứng minh OI vuông góc với MN
a: Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét ΔABC có
BN là đường cao
CM là đường cao
BN cắt CM tại H
Do đó: AH\(\perp\)BC
Cho tam giác ABC nhọn , dựng đường tròn tâm O đường kính BC , đường tròn (O) cắt các cạnh AB , AC lần lượt tại M và N , BN cắt CM tại H . Chứng minh AH vuông góc với BC
Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đo: ΔBNC vuông tại N
Xet ΔABC có
BN,CM là các đường cao
BN cắt CM tại H
Do đó; H là trực tâm
=>AH vuông góc với BC
1 .
Cho tam giác ABC vuông tại A, đường cao AH. Vẽ đường tròn tâm I, đường kính AH cắt AB, AC lần lượt tại M và N, D là giao điểm của MN và OA
a) chứng minh AM.AB=AN.AC và tứ giác BMNC nội tiếp
b) cm tam giác ADI đồng dạng tam giác AHO
c) gọi E là giao điểm BC và NM, K là giao điểm AE và (I). cm góc BKC = 90°
2 .
Cho tam giác ABC nhọn, BC = AC, đường tròn tâm O đường kính BC cắt AB,AC tại E,F. BF cắt CE tại H, AH cắt BC tại D.
a) Chứng minh: AD vuông góc BC
b) Chứng minh: AD là đường phân giác của góc EDF
c) Đường tròn đường kính EC cắt AC tại M, BM cắt (O) tại K. Chứng minh: KC đi qua trung điểm của HF
ối chồi em mới lớp 7 thôi
cho tam giác abc nhọn. vẽ nửa đường tròn tâm o đường kính bc cắt cạnh ab và ac thứ tự tại m và n. gọi h là giao điểm của bn và cm.
a)cm ah vuông góc với bc
b)chứng minh 4 điểm a,m,h,n cùng thuộc một đường tròn. xác định tâm i của đường tròn đó
c)chứng minh om là tiếp tuyến của đường tròn tâm i
a: Xét (O) có
ΔBMC nộitiếp
BC là đường kính
=>ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
=>ΔBNC vuông tại N
Xét ΔABC có
BN,CM là các đường cao
BN cắt CM tại H
=>H là trực tâm
=>AH vuông góc với BC
b: Xét tứ giác AMHN có
góc AMH+góc ANH=180 độ
=>AMHN là tứ giác nội tiếp
I là trung điểm của AH
c: góc IMO=góc IMH+góc OMH
=góc IHM+góc OCH
=90 độ-góc BAH+góc BCM
=90 độ
=>OM là tiếp tuyến của (I)
Cho tam giác ABC nhọn . Vẽ đường tròn đường kính BC cắt AB tại M , AC tại N .
a. Chứng minh BN vuông với AC , CM vuông góc với AB.
b. Gọi H là giao điểm của BN và CM. Chứng minh AH vuông với BC.
a: Xét \(\left(O\right)\) có
\(\widehat{CNB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{CNB}=90^0\)
hay CM\(\perp\)AB
Xét \(\left(O\right)\) có
\(\widehat{BNC}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{BNC}=90^0\)
hay BN\(\perp\)AC
b: Xét ΔABC có
BN là đường cao ứng với cạnh AC
CM là đường cao ứng với cạnh AB
BN cắt CM tại H
Do đó: AH\(\perp\)BC
Cho tam giác nhọn ABC . Vẽ đường tròn tâm O đường kính BC, nó cắt các cạnh AB, AC theo thứ tự ở M, N
a/ Chứng minh rằng CM vuông góc AB, BN vuông góc AC
b/ Gọi H là giao điểm của BN và CM . Chứng minh rằng AH vuông góc BC
Cho tam giác ABC có ba góc nhọn (AB<AC). Đường tròn tâm O đường kính BC cắt các cạnh AB, AC lần lượt tại D, E. Gọi H là giao điểm của BE và CD , F là giao điểm của AH và BC. a) Tính số đo góc BDC và chứng minh AF vuông tại BC b) Gọi K là trung điểm của AH. Chứng minh KE là tiếp tuyến của đường tròn (O) c) Gọi N là giao điểm của đoạn thẳng AF và đường tròn (O). Chứng minh FN bình-FH bình=2FH.HK
(Mong mọi người giúp mình ạ)
a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: AH⊥BC
hay AF⊥BC
CM CÂU C THÔI NHÁ
cho tam giác abc nhọn, đường tròn (O) đường kính bc cắt ab, ac lần lượt tại E và f. gọi h là giao điểm của bf và ce, ah cắt bc tại d.
a) chứng minh ah vuông góc với bc và tứ giác aehf nội tiếp, xác định tâm K của đường tròn này.
b) chứng minh ke là tiếp tuyến của đường tròn (O) và năm điểm o, d, e, k, f cùng thuộc một đường tròn
c) qua h vẽ đường thẳng vuông góc ho cắt ab, ac lần lượt tại m và n. chứng minh hm=hn
c: Theo câu b, ta được: H là tâm đường tròn ngoại tiếp ngũ giác DEKFO
OH vuông góc MN
=>MN là đường kính của (H)
=>HM=HN
Cho tam giác nhọn ABC (AB < AC). Đường tròn tâm O đường kính BC cắt AB và AC lần lượt tại E và D. Gọi H là giao điểm của BD và CE; AH cắt BC tại I.
a) Chứng minh AI vuông góc với BC và EC là phân giác của góc IED.
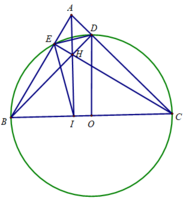
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)

Cho tam giác ABC nhọn. Đường tròn tâm O đường kính BC cắt AB ở M và cắt AC ở N. Gọi H là giao điểm của BN và CM, E là trung điểm AH.
a) Chứng minh H là trực tâm của tam giác ABC.
b) Chứng minh ME là tiếp tuyến của đường tròn (O).
c) Chứng minh MN. OE = 2ME. MO
Lời giải:
a. Ta có:
$\widehat{BNC}=\widehat{BMC}=90^0$ (góc nt chắn nửa đường tròn - cung BC)
$\Rightarrow BN\perp AC, CM\perp AB$
Tam giác $ABC$ có 2 đường cao $BN, CM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $ABC$.
b. Gọi $D$ là giao của $AH$ và $BC$. Do $H$ là trực tâm tam giác $ABC$ nên $AH\perp BC$ tại $D$.
Tam giác $BMC$ vuông tại $M$
$\Rightarrow$ trung tuyến $MO= \frac{BC}{2}=BO$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow BOM$ là tam giác cân tại $O$
$\Rightarrow \widehat{OMB}=\widehat{OBM}=90^0-\widehat{BCM}$
$=90^0-\widehat{DCH}=\widehat{MHA}=\widehat{MHE}(1)$
$CM\perp AB$ nên $AMH$ là tam giác vuông tại $M$
$\Rightarrow ME=\frac{AH}{2}=EH$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow MEH$ cân tại $E$
$\Rightarrow \widehat{MHE}=\widehat{EMH}(2)$
Từ $(1); (2)\Rightarrow \widehat{OMB}=\widehat{EMH}$
$\Rightarrow \widehat{OMB}+\widehat{OMC}=\widehat{EMH}+\widehat{OMC}$
$\Rightarrow \widehat{BMC}=\widehat{EMO}$
$\Rightarrow \widehat{EMO}=90^0$
$\Rightarrow EM\perp MO$ nên $EM$ là tiếp tuyến $(O)$
c.
Ta có:
$EM=\frac{AH}{2}=EN$
$OM=ON$
$\Rightarrow EO$ là trung trực của $MN$
Gọi $T$ là giao điểm $EO, MN$ thì $EO\perp MN$ tại $T$ và $T$ là trung điểm $MN$.
Xét tam giác $EMO$ vuông tại $M$ có $MT\perp EO$ thì:
$ME.MO = MT.EO = \frac{MN}{2}.EO$
$\Rightarrow 2ME.MO = MN.EO$