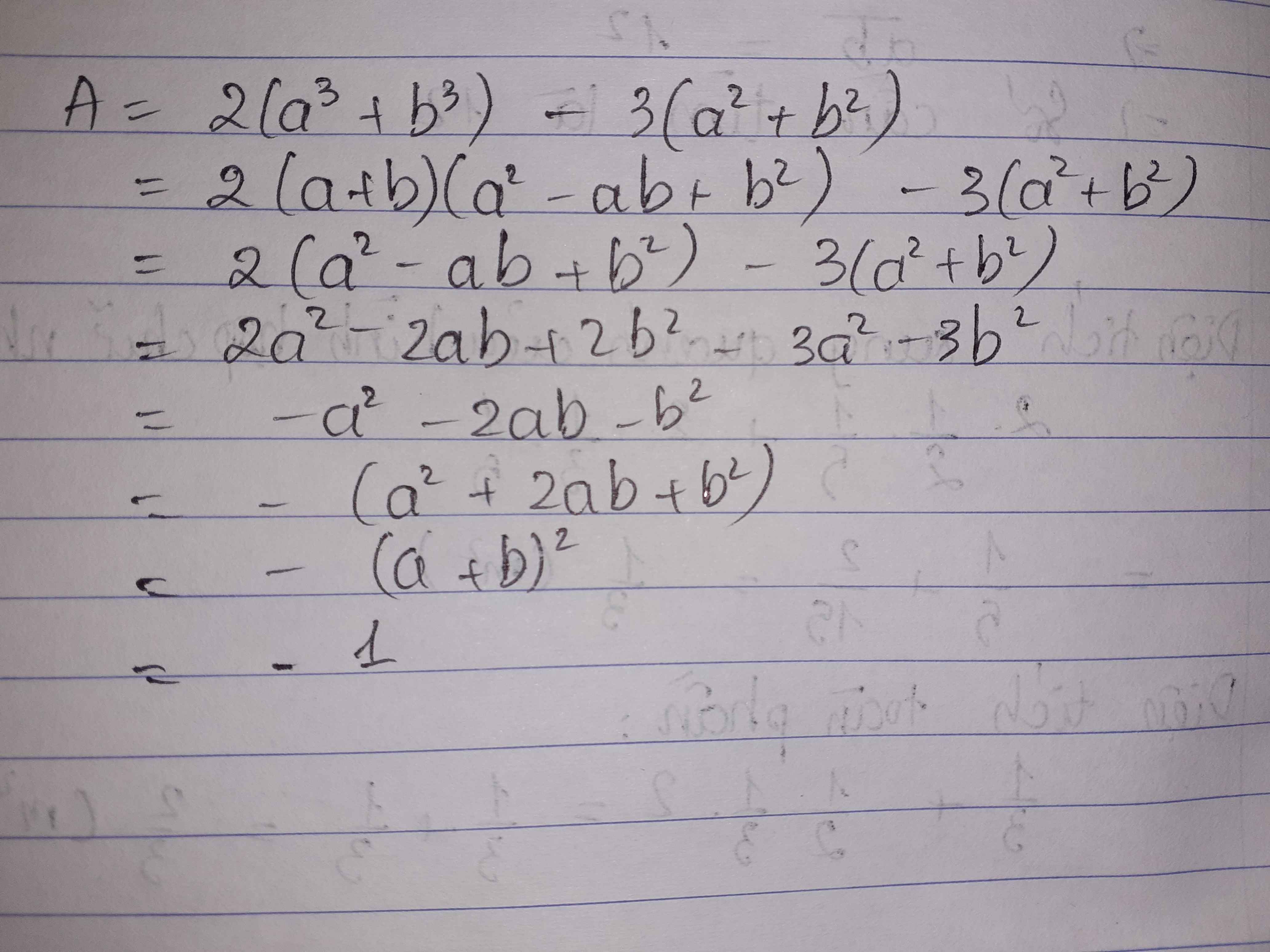cho a+b=1. Tính M=\(2\left(a^3+b^3\right)-3\left(a^2+b^2\right)\)

Những câu hỏi liên quan
Cho a+b=1.Tính
M=\(2\left(a^3+b^3\right)-3\left(a^2+b^2\right)\)
\(M=2\left(a+b\right)\left(a^2-ab+b^2\right)-3\left(a^2+b^2\right)\)
\(=2\left(a^2-ab+b^2\right)-3\left(a^2+b^2\right)=2a^2-2ab+2b^2-3a^2-3b^2\)
\(=-a^2-2ab-b^2=-\left(a^2+2ab+b^2\right)=-\left(a+b\right)^2=-1^2=-1\)
Đúng 0
Bình luận (0)
\(M=2\left(a^3+b^3\right)-3\left(a^2+b^2\right)\)
\(=2a^3+2b^3-3a^2-3b^2\)
\(=a^2\left(2a-3\right)+b^2\left(2b-3\right)\)
\(=a^2\left[2a-3\left(a+b\right)\right]+b^2\left[2b-3\left(a+b\right)\right]\) (do a+b=1 )
\(=a^2\left(2a-3a-3b\right)+b^2\left(2b-3a-3b\right)\)
\(=a^2\left(-a-3b\right)+b^2\left(-b-3a\right)\)
\(=-a^3-3a^2b-b^3-3ab^2\)
\(=-\left(a^3+3a^2b+3ab^2+b^3\right)\)
\(=-\left(a+b\right)^3\)
\(=-3\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho
\(A=\dfrac{1}{2}+\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3}{2}\right)^3+\left(\dfrac{3}{2}\right)^4+...+\left(\dfrac{3}{2}\right)^{2021}\)
\(B=\left(\dfrac{3}{2}\right)^{2013}:2\)
tính B-A
Ta có \(A=\dfrac{1}{2}+\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3}{2}\right)^3+\left(\dfrac{3}{2}\right)^4+...+\left(\dfrac{3}{2}\right)^{2021}\left(1\right)\)
\(\Rightarrow\dfrac{3}{2}A=\dfrac{3}{4}+\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3}{2}\right)^3+\left(\dfrac{3}{2}\right)^4+...+\left(\dfrac{3}{2}\right)^{2013}\left(2\right)\)
Lấy (2) - (1) ta được:
\(\dfrac{3}{2}A-A=\left(\dfrac{3}{2}\right)^{2013}+\dfrac{3}{4}-\dfrac{1}{2}-\dfrac{3}{2}\)
\(\dfrac{1}{2}A=\left(\dfrac{3}{2}\right)^{2013}+\dfrac{1}{4}\Rightarrow A=\dfrac{3^{2013}}{2^{2012}}+\dfrac{1}{2}\)
Vậy \(B-A=\dfrac{3^{2013}}{2^{2014}}-\dfrac{3^{2013}}{2^{2012}}+\dfrac{5}{2}\)
Đúng 1
Bình luận (0)
Cho a + b = 1. Tính A = 2\(\left(a^3+b^3\right)\) - 3\(\left(a^2+b^2\right)\).
\(A=2\left(a+b\right)^3-6ab\left(a+b\right)-3\left(a+b\right)^2+6ab\)
\(=2-6ab-3+6ab=-1\)
Đúng 6
Bình luận (0)
Tính \(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\) biết a+b=1
\(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)+3ab\left[\left(a+b\right)^2-2ab\right]+6a^2b^2\)
\(=1-3ab+3ab\left[1-2ab\right]+6a^2b^2\)
\(=1-3ab+3ab-6a^2b^2+6a^2b^2\)
=1
Đúng 2
Bình luận (0)
Rút gọn :
a,Aleft(3+1right)left(3^2+1right)left(3^4+1right)...left(3^{64}+1right)
b,B-1^2+2^2-3^2+4^2-...-99^2+100^2
c,C-1^2+2^2-3^2+4^2-...+left(-1right)^ncdot n^2
d,D3cdotleft(2^2+1right)left(2^4+1right)...left(2^{64}+1right)+1
e,Eleft(a+b+cright)^2+left(a+b-cright)^2-2left(a+bright)^2
g,Gleft(a+b+c+dright)^2+left(a+b-c-dright)^2+left(a+c-b-dright)^2+left(a+d-b-cright)^2
h,Hleft(a+b+cright)^3-left(b+c-aright)^3-left(a+c-bright)^3+left(a+b-cright)^3
i,Ileft(a+bright)^3+left(b+cright)^3+left(c...
Đọc tiếp
Rút gọn :
\(a,A=\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\\ b,B=-1^2+2^2-3^2+4^2-...-99^2+100^2\\ c,C=-1^2+2^2-3^2+4^2-...+\left(-1\right)^n\cdot n^2\\ d,D=3\cdot\left(2^2+1\right)\left(2^4+1\right)...\left(2^{64}+1\right)+1\\ e,E=\left(a+b+c\right)^2+\left(a+b-c\right)^2-2\left(a+b\right)^2\\ g,G=\left(a+b+c+d\right)^2+\left(a+b-c-d\right)^2+\left(a+c-b-d\right)^2+\left(a+d-b-c\right)^2\\ h,H=\left(a+b+c\right)^3-\left(b+c-a\right)^3-\left(a+c-b\right)^3+\left(a+b-c\right)^3\\ i,I=\left(a+b\right)^3+\left(b+c\right)^3+\left(c+a\right)^3-3\left(a+b\right)\left(c+b\right)\left(c+a\right)\)
Mọi người ơi, giúp mk vs, đc câu nào hay câu ấy ! Help me!!!!!!!!!!!!!!!!!!
a/ \(A=\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\)
\(2A=2\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\)
\(2A=\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\)
\(2A=\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\)
\(2A=\left(3^4-1\right)\left(3^4+1\right)...\left(3^{64}+1\right)\)
\(\Rightarrow2A=3^{128}-1\Rightarrow A=\dfrac{3^{128}-1}{2}\)
Đúng 0
Bình luận (1)
e) ta dể dàng thấy được : \(a^2+b^2=\left(a+b\right)^2-2ab\)
\(\Rightarrow E=\left(a+b+c\right)^2+\left(a+b-c\right)^2-2\left(a+b\right)^2\)
\(=\left(2a+2b\right)^2-2\left(a+b+c\right)\left(a+b-c\right)-2\left(a+b\right)^2\)
\(=4\left(a+b\right)^2-2\left(\left(a+b\right)^2-c^2\right)-2\left(a+b\right)^2\)
\(=4\left(a+b\right)^2-2\left(a+b\right)^2+2c^2-2\left(a+b\right)^2=2c^2\)
g) củng sử dụng cái trên ta có : \(G=\left(a+b+c+d\right)^2+\left(a+b-c-d\right)^2+\left(a+c-b-d\right)^2+\left(a+d-b-c\right)^2\)
\(=\left(2a+2b\right)^2-2\left(a+b+c+d\right)\left(a+b-c-d\right)+\left(2a-2b\right)^2-2\left(a+c-b-d\right)\left(a+d-b-c\right)\)
\(=4\left(a+b\right)^2+4\left(a-b\right)^2-2\left(\left(a+b\right)^2-\left(c+d\right)^2\right)-2\left(\left(a-b\right)^2-\left(c-d\right)^2\right)\)
\(=4\left(\left(a+b\right)^2+\left(a-b\right)^2\right)-2\left(\left(a+b\right)^2+\left(a-b\right)^2\right)+2\left(\left(c+d\right)^2+\left(c-d\right)^2\right)\)
\(=2\left(\left(a+b\right)^2+\left(a-b\right)^2\right)+2\left(\left(c+d\right)^2+\left(c-d\right)^2\right)\)\(=2\left(\left(2a\right)^2-2\left(a+b\right)\left(a-b\right)\right)+2\left(\left(2c\right)^2-2\left(c+d\right)\left(c-d\right)\right)\)
\(=2\left(4a^2-2\left(a^2-b^2\right)\right)+2\left(4c^2-2\left(c^2-d^2\right)\right)\)
\(=2\left(2a^2+2b^2\right)+2\left(2c^2+2d^2\right)=4\left(a^2+b^2+c^2+d^2\right)\)
bn đăng nhiều quá nên mk làm câu nào hay câu đó nha
mà nè mấy câu a;b;c;d hình như trên mạng có bn lên đó tìm nha .
Đúng 0
Bình luận (4)
Xem thêm câu trả lời
Cho a+b+c\(a^3+b^3+c^3=3abc\) áp dụng tính B=\(\frac{\left(a^2-b^2\right)^3+\left(b^2-c^2\right)^3+\left(c^2-a^2\right)^3}{\left(a-b\right)^3+\left(b-c\right)^3+\left(c-a\right)^3}\)
1. Cho a2 - b2 - c2 =3abc
Tính H = \(\left(1-\frac{a}{b}\right)\left(1-\frac{b}{c}\right)\left(1-\frac{c}{a}\right)\)
2. Cho a - b + c = - 4
Tính B = \(\frac{a^3-b^3+c^3+3abc}{\left(a+b\right)^2+\left(b+c\right)^2+\left(c-a\right)^2}\)
Cho a+b=1
Tính \(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b)
= (a + b)(a2 - ab + b2) + 3ab((a + b)2 - 2ab) + 6a2b2(a + b)
= (a + b)((a + b)2 - 3ab) + 3ab((a + b)2 - 2ab) + 6a2b2(a + b)
= 1 - 3ab + 3ab(1 - 2ab) + 6a2b2
= 1 - 3ab + 3ab - 6a2b2 + 6a2b2 = 1
Đúng 0
Bình luận (0)
cho a+b=1
tính \(M=a^3+b^3+3ab\left(a^2+b^2\right)+6a^2b^2\left(a+b\right)\)
Có: M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b)
=> M = (a + b)(a2 - ab + b2) + 3ab((a + b)2 - 2ab) + 6a2b2(a + b)
=> M = (a + b)[(a + b)2 - 3ab] + 3ab[(a + b)2 - 2ab] + 6a2b2(a + b)
=> M = 1 - 3ab + 3ab(1 - 2ab) + 6a2b2 (vì a+b=1)
=> M = 1 - 3ab + 3ab - 6a2b2 + 6a2b2
=> M = 1
Vậy M = 1
M = \(a^3\)+ \(b^3\)+ 3ab ( \(a^2\)+ \(b^2\)) + \(6a^2\)\(b^2\)(a+b)
M = ( a + b ) ( \(a^2\)- ab + \(b^2\)) + 3ab [ \(a^2\)+ \(b^2\)+ 2ab( a + b )
M = \(a^2\)- ab + \(b^2\)+ 3ab ( \(a^2\)+ 2ab + \(b^2\))
Với a + b = 1
M= \(a^2\)- ab + \(b^2\)+ 3ab\(\left(a+b\right)^2\)
M = \(a^2\)- ab + \(b^2\)+ 3ab
M = \(a^2\)+ \(b^2\)+ 2ab
M = \(a^2\)+ 2ab + \(b^2\)
M = \(\left(a+b\right)^2\)
M = 1
Vậy M = 1