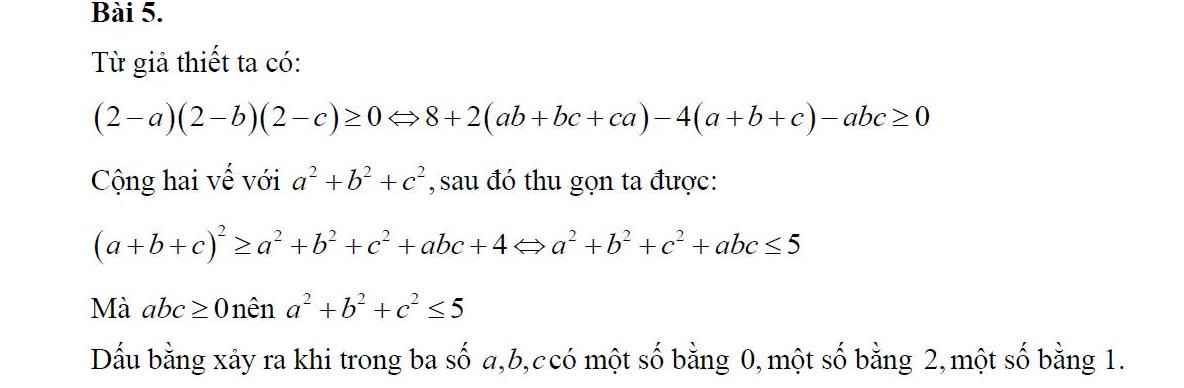Cho a/x=b/x+1=c/x+2.Cmr:4(a-b)(b-c)=(a-c)^2

Những câu hỏi liên quan
1.Cho a,b,c là độ dài ba cạnh của một tam giác:
CMR: \(a^2+b^2+c^2\leq2(ab+bc+ac)\)
2.CMR: \((x-1)(x-2)(x-3)(x-4)\geq-1\)
3.CMR:\(a^4+b^4+c^4\geq abc( a+b+c)\)
1. Không có dấu "=" em nhé.
Vì $a,b,c$ là độ dài 3 cạnh tam giác nên theo BĐT tam giác thì:
$a< b+c\Rightarrow a^2< ab+ac$
$b< a+c\Rightarrow b^2< ba+bc$
$c< a+b\Rightarrow c^2< ca+cb$
$\Rightarrow a^2+b^2+c^2< 2(ab+bc+ac)$
Ta có đpcm.
Đúng 3
Bình luận (2)
2.
$(x-1)(x-2)(x-3)(x-4)$
$=(x-1)(x-4)(x-2)(x-3)$
$=(x^2-5x+4)(x^2-5x+6)$
$=(x^2-5x+4)(x^2-5x+4+2)$
$=(x^2-5x+4)^2+2(x^2-5x+4)$
$=(x^2-5x+4)^2+2(x^2-5x+4)+1-1$
$=(x^2-5x+5)^2-1\geq 0-1=-1$ do $(x^2-5x+5)^2\geq 0$ với mọi $x\in\mathbb{R}$
Vậy ta có đpcm.
Đúng 2
Bình luận (0)
3.
Áp dụng BĐT Cô-si:
$a^4+b^4\geq 2a^2b^2$
$b^4+c^4\geq 2b^2c^2$
$c^4+a^4\geq 2c^2a^2$
Cộng theo vế và thu gọn thì:
$a^4+b^4+c^4\geq a^2b^2+b^2c^2+c^2a^2(*)$
Tiếp tục áp dụng BĐT Cô-si:
$a^2b^2+b^2c^2\geq 2|ab^2c|\geq 2ab^2c$
$b^2c^2+c^2a^2\geq 2abc^2$
$a^2b^2+c^2a^2\geq 2a^2bc$
Cộng theo vế và thu gọn:
$\Rightarrow a^2b^2+b^2c^2+c^2a^2\geq abc(a+b+c)(**)$
Từ $(*); (**)\Rightarrow a^4+b^4+c^4\geq abc(a+b+c)$
Dấu "=" xảy ra khi $a=b=c$
Đúng 3
Bình luận (0)
toàn bộ dùng bất đẳng thức svac-xơ hoặc bunhiacopskibài 1: cho x,y,z0. CMR:a,1/x+1/y4/x+yb,1/x+1/y+1/z9/x+y+zbài 2: cho a,b,c0. CMR:a,a^2/(b+c)+b^2/(c+a)+c^2/(a+b)(a+b+c)/2b, a^2/(2b+5c)+b^2/(2c+5a)+c^2/(2a+5b)(a+b+c)/7bài 3: cho a,b,c0. CMR a/(b+c)+b/(c+a)+c/(b+a)3/2bài 4: cho a,b,c0. CMR:1/(b+2c)+b/(c+2a)+c/(a+2b)1bài 5: cho a+b+c1. Tìm mina, P1/a+4/b+9/cb, Q+a^2/(b+3c)+b^2/(c+3a)+c^2/(a+3b)bài 6: cho 3x^2+5y^23/79tìm max, min Ax+4ybài 7: tìm min P,Q,Ra, P1/x+1/x;x0b, Qx+1/x;x3c, R1/x+4/(1-x);...
Đọc tiếp
toàn bộ dùng bất đẳng thức svac-xơ hoặc bunhiacopski
bài 1: cho x,y,z>0. CMR:
a,1/x+1/y>=4/x+y
b,1/x+1/y+1/z>=9/x+y+z
bài 2: cho a,b,c>0. CMR:
a,a^2/(b+c)+b^2/(c+a)+c^2/(a+b)>=(a+b+c)/2
b, a^2/(2b+5c)+b^2/(2c+5a)+c^2/(2a+5b)>=(a+b+c)/7
bài 3: cho a,b,c>0. CMR a/(b+c)+b/(c+a)+c/(b+a)>=3/2
bài 4: cho a,b,c>0. CMR:
1/(b+2c)+b/(c+2a)+c/(a+2b)>=1
bài 5: cho a+b+c=1. Tìm min
a, P=1/a+4/b+9/c
b, Q+a^2/(b+3c)+b^2/(c+3a)+c^2/(a+3b)
bài 6: cho 3x^2+5y^2=3/79
tìm max, min A=x+4y
bài 7: tìm min P,Q,R
a, P=1/x+1/x;x>0
b, Q=x+1/x;x>=3
c, R=1/x+4/(1-x);0<x<1
bài 8: cho a,b,c là 3 cạnh một tam giác. CMR
a, a/(b+c-a)+b/(c+a-b)+c/(a+b-c)>=3
b, tìm min P
P=a/(b+c-a)+4b/(c+a-b)+9c/(a+b-c)
toàn bộ dùng bất đẳng thức svac-xơ hoặc bunhiacopski
bài 1: cho x,y,z0. CMR:
a,1/x+1/y4/x+y
b,1/x+1/y+1/z9/x+y+z
bài 2: cho a,b,c0. CMR:
a,a^2/(b+c)+b^2/(c+a)+c^2/(a+b)(a+b+c)/2
b, a^2/(2b+5c)+b^2/(2c+5a)+c^2/(2a+5b)(a+b+c)/7
bài 3: cho a,b,c0. CMR a/(b+c)+b/(c+a)+c/(b+a)3/2
bài 4: cho a,b,c0. CMR:
1/(b+2c)+b/(c+2a)+c/(a+2b)1
bài 5: cho a+b+c1. Tìm min
a, P1/a+4/b+9/c
b, Q+a^2/(b+3c)+b^2/(c+3a)+c^2/(a+3b)
bài 6: cho 3x^2+5y^23/79
tìm max, min Ax+4y
bài 7: tìm min P,Q,R
a, P1/x+1/...
Đọc tiếp
toàn bộ dùng bất đẳng thức svac-xơ hoặc bunhiacopski
bài 1: cho x,y,z>0. CMR:
a,1/x+1/y>=4/x+y
b,1/x+1/y+1/z>=9/x+y+z
bài 2: cho a,b,c>0. CMR:
a,a^2/(b+c)+b^2/(c+a)+c^2/(a+b)>=(a+b+c)/2
b, a^2/(2b+5c)+b^2/(2c+5a)+c^2/(2a+5b)>=(a+b+c)/7
bài 3: cho a,b,c>0. CMR a/(b+c)+b/(c+a)+c/(b+a)>=3/2
bài 4: cho a,b,c>0. CMR:
1/(b+2c)+b/(c+2a)+c/(a+2b)>=1
bài 5: cho a+b+c=1. Tìm min
a, P=1/a+4/b+9/c
b, Q+a^2/(b+3c)+b^2/(c+3a)+c^2/(a+3b)
bài 6: cho 3x^2+5y^2=3/79
tìm max, min A=x+4y
bài 7: tìm min P,Q,R
a, P=1/x+1/x;x>0
b, Q=x+1/x;x>=3
c, R=1/x+4/(1-x);0<x<1
bài 8: cho a,b,c là 3 cạnh một tam giác. CMR
a, a/(b+c-a)+b/(c+a-b)+c/(a+b-c)>=3
b, tìm min P
P=a/(b+c-a)+4b/(c+a-b)+9c/(a+b-c)
a) cho x,y dương. CMR: \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
b) cho a+b+c=1 CMR: \(\frac{a}{a+b^2}+\frac{b}{b+c^2}+\frac{c}{c+a^2}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
a/ \(\Leftrightarrow\frac{x+y}{xy}\ge\frac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)
\(\Leftrightarrow x^2+y^2-2xy\ge0\Leftrightarrow\left(x-y\right)^2\ge0\) (luôn đúng)
Vậy BĐT đã cho đúng
b/ \(\frac{a}{a+b^2}=\frac{a}{a\left(a+b+c\right)+b^2}=\frac{a}{a^2+b^2+a\left(b+c\right)}\le\frac{a}{2ab+a\left(b+c\right)}=\frac{1}{b+b+b+c}\)
\(\Rightarrow\frac{a}{a+b^2}=\frac{1}{b+b+b+c}\le\frac{1}{16}\left(\frac{1}{b}+\frac{1}{b}+\frac{1}{b}+\frac{1}{c}\right)=\frac{1}{16}\left(\frac{3}{b}+\frac{1}{c}\right)\)
Tương tự: \(\frac{b}{b+c^2}\le\frac{1}{16}\left(\frac{3}{c}+\frac{1}{a}\right)\) ; \(\frac{c}{c+a^2}\le\frac{1}{16}\left(\frac{3}{a}+\frac{1}{c}\right)\)
Cộng vế với vế:
\(VT\le\frac{1}{16}\left(\frac{4}{a}+\frac{4}{b}+\frac{4}{c}\right)=\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Dấu "=" xảy ra khi \(a=b=c=\frac{1}{3}\)
Đúng 0
Bình luận (0)
1 Cho a+b+c =0; a^2+b^2+c^2 =1.CMR a^4+b^4+c^4=1/2
2Cho a^2-b^2=4c^2 CMR (5a-3b+8c)(5a-3b-8c)=(3a-5b)^2
3 CMR Nếu (a^2+b^2)(x^2+y^2)=(ax+by)^2 với x,y khác o thì a/x=b/y
1. Cho a,b,c,x,y,z khác 0 thỏa mãn:frac{7cy-5bz}{x}frac{2az-7cx}{y}frac{5bx-2ay}{z}CMR: frac{2a}{x}frac{5b}{y}frac{7c}{z}2.Cho a,b,c,x,y,z khác 0 thỏa mãn: frac{x}{a}frac{y}{b}frac{z}{c}CMR: frac{x^2+y^2+z^2}{left(ax+by+czright)^2}frac{1}{a^2+b^2+c^2}3.Cho a,b,c thỏa mãn frac{a}{2016}frac{b}{2017}frac{c}{2018}CMR: 4(a-b)(b-c)(a-c)24. Cho a,b,c thỏa mãn:frac{a}{x}frac{b}{x+1}frac{c}{x+2}CMR: 4(a-b)(b-c)(a-c)25. Cho a,b,c thỏa mãn:frac{a}{-2017}frac{b}{-2016}frac{c}{-2015}CMR: 4(a-b)(b-c)(a-c)26....
Đọc tiếp
1. Cho a,b,c,x,y,z khác 0 thỏa mãn:
\(\frac{7cy-5bz}{x}=\frac{2az-7cx}{y}=\frac{5bx-2ay}{z}\)
CMR: \(\frac{2a}{x}=\frac{5b}{y}=\frac{7c}{z}\)
2.Cho a,b,c,x,y,z khác 0 thỏa mãn: \(\frac{x}{a}=\frac{y}{b}=\frac{z}{c}\)
CMR: \(\frac{x^2+y^2+z^2}{\left(ax+by+cz\right)^2}=\frac{1}{a^2+b^2+c^2}\)
3.Cho a,b,c thỏa mãn \(\frac{a}{2016}=\frac{b}{2017}=\frac{c}{2018}\)
CMR: 4(a-b)(b-c)=(a-c)2
4. Cho a,b,c thỏa mãn:\(\frac{a}{x}=\frac{b}{x+1}=\frac{c}{x+2}\)
CMR: 4(a-b)(b-c)=(a-c)2
5. Cho a,b,c thỏa mãn:
\(\frac{a}{-2017}=\frac{b}{-2016}=\frac{c}{-2015}\)
CMR: 4(a-b)(b-c)=(a-c)2
6. Cho a,b,c khác 0 và \(\frac{b+c+a}{a}=\frac{a+b-c}{b}=\frac{c+a-b}{c}\)
Tính giá trị biểu thức A=\(\frac{\left(a-b\right)\left(c+b\right)\left(c-a\right)}{abc}\)
1/CMR
a/x^4-2x^3+2x^2-2x+1ge0forall xin R
b/cho age0,bge2,a+b+c3. CMR : a^2+b^2+c^2le5
c/cho a,b,c 0 . CMR : frac{b+c}{a}+frac{a+c}{b}+frac{a+b}{c}ge4left(frac{a}{b+c}+frac{b}{a+c}+frac{c}{a+b}right)
2/ cho x,yge0,x+y1. tìm GTLN,GTNN của A x^2+y^2
3/ cho x,y0 .tìm GTNN của B frac{left(x+yright)^2}{x^2+y^2}+frac{left(x+yright)^2}{xy}
Đọc tiếp
1/CMR
a/\(x^4-2x^3+2x^2-2x+1\ge0\forall x\in R\)
b/cho \(a\ge0,b\ge2,a+b+c=3\). CMR : \(a^2+b^2+c^2\le5\)
c/cho a,b,c >0 . CMR : \(\frac{b+c}{a}+\frac{a+c}{b}+\frac{a+b}{c}\ge4\left(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}\right)\)
2/ cho \(x,y\ge0,x+y=1\). tìm GTLN,GTNN của A =\(x^2+y^2\)
3/ cho x,y>0 .tìm GTNN của B= \(\frac{\left(x+y\right)^2}{x^2+y^2}+\frac{\left(x+y\right)^2}{xy}\)
B1: Cho 0le a,b,cle2 thỏa mãn a+b+c3. CMR: a^2+b^2+c^2le5B2: Cho a,bge0 thỏa mãn a^2+b^2a+b. TÌm GTLN Sdfrac{a}{a+1}+dfrac{b}{b+1}B3: CMR: dfrac{1}{left(x-yright)^2}+dfrac{1}{x^2}+dfrac{1}{y^2}gedfrac{4}{xy}forall xne y,xyne0
Đọc tiếp
B1: Cho \(0\le a,b,c\le2\) thỏa mãn \(a+b+c=3\). CMR: \(a^2+b^2+c^2\le5\)
B2: Cho \(a,b\ge0\) thỏa mãn \(a^2+b^2=a+b\). TÌm GTLN \(S=\dfrac{a}{a+1}+\dfrac{b}{b+1}\)
B3: CMR: \(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\forall x\ne y,xy\ne0\)
Bài 3:
\(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\)
\(\Leftrightarrow x^2y^2\left(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)\ge\dfrac{4}{xy}.x^2y^2\)
\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2+y^2\ge4xy\)
\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2-2xy+y^2\ge2xy\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2+\left(x-y\right)^2\ge2xy\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2-2xy+\left(x-y\right)^2\ge0\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}-x+y\right)^2=0\) (luôn đúng)
Đúng 4
Bình luận (4)
a) Cho dãy tỉ số bằng nhau a/2009=b/2011=c/2013
cmr: (a-c)2/4= ( a-b)(b-c)
b) Cho đa thức f(x) thỏa mãn điều kiện x.f(x+1)=(x+2)f(x)
cmr: đa thức f(x) có ít nhất 2 nghiệm