Cho tứ giác ABCD có AB=CD, AD=BC.Chứng minh AB song song với CD

Những câu hỏi liên quan
Cho tứ giác ABCD có AB=CD, AD=BC.Chứng minh AB ssong song CD
1/Cho tứ giác ABCD có AB//CD,AD//BC.Chứng minh AD=BC,AB=CD.
2/Cho tứ giác ABCD có AB//CD,AB=CD.Chứng minh AD//BC và AD=BC
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
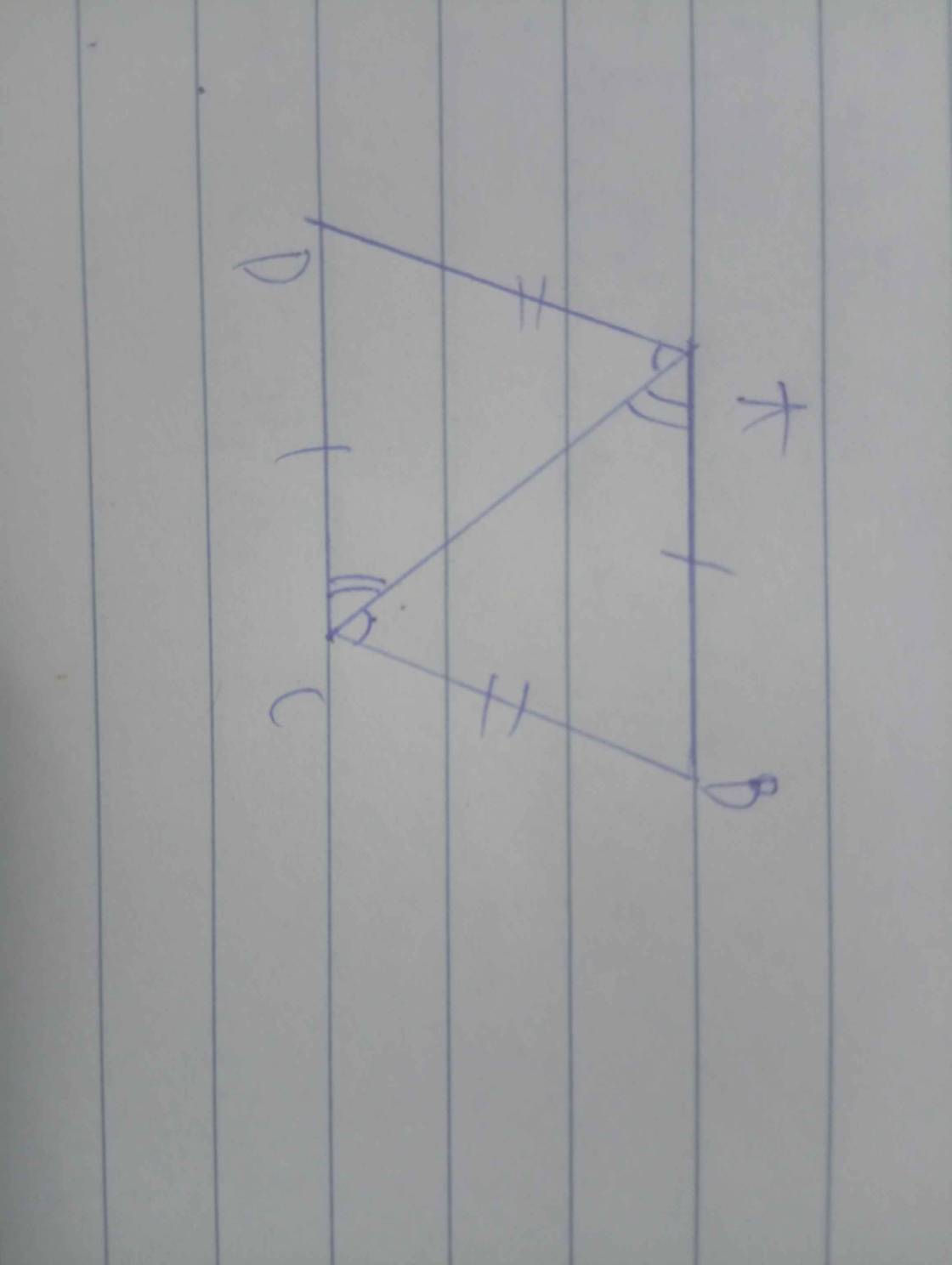
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AB song song với CD và AB = CD
C/m : AD = BC và AD song song với BC
\(\text{AB song song với CD và AB=CD}\Rightarrow ABCD\text{ là hình bình hành}\)
\(\Rightarrow AD\text{//}BC\text{ và }AD=BC\)
Cho tứ giác ABCD có AB=CD và AB,CD không song song với nhau. Chứng minh rằng đường thẳng đi qua trung điểm các cạnh BC và AD tạo với đường thẳng AB và CD những góc nhọn bằng nhau.
Tham khảo nha, tuy ko trùng đề lắm
Gọi trung điểm dường cheo AC, BD lần lượt là M, N
MN cắt AB, CD lần lượt ở I, K
Ta cần chứng minh góc NIB = góc MKC
Lấy H là trung điểm BC. Nối MH, NH.
Xét tam giac ABC có AM = MC ; CH = HB => MH là đường trung bình tam giác ABC => MH =AB/2 (1) và MH // AB => góc KMH = góc INH (2)
chung minh tuong tu ta có: NH = CD/2 (3)và NH // CD =>góc INH = góc MKC (4)
Mat khac từ (1)và (3) ta có NH = MH vì đều bằng một nửa AB và CD => tam giác MHN cân tại H => góc NMH = góc MNH =>góc KMH = góc INH (vì kể với 2 góc bằng nhau) (5)
Từ (3)(4)(5) => góc MKC = góc NIB (đpcm)
Đúng 2
Bình luận (0)
Cho tứ giác ABCD, AB không song song với CD; M, N lần lượt là trung điểm của BC, AD. Chứng minh \(MN=\dfrac{AB+CD}{2}\)
Đề sai rồi, phải là cm \(MN< \dfrac{AB+CD}{2}\)
Đúng 5
Bình luận (0)
Cho tứ giác ABCD có (O) đường kính AB tiếp xúc với CD. Chứng minh (I) đường kính CD tiếp xúc với AB\(\Leftrightarrow\)AD song song với BC
+) Chứng minh nếu AD // BC thì đường tròn (I) đường kính CD tiếp xúc AB:
Gọi tiếp điểm giữa (O) và CD là H .Từ I hạ IK vuông góc AB tại K.
Khi đó tứ giác KOHI nội tiếp đường tròn (OI) => ^KHI = ^KHD = ^KOI
Dễ thấy tứ giác ABCD là hình thang (Vì BC // AD) có đường trung bình OI nên OI // BC // AD
=> ^KOI = ^KBC. Do đó ^KHD = ^KBC => Tứ giác BKHC nội tiếp. Tương tự, tứ giác ADHK nội tiếp
Từ đó ^DKC = ^DKH + ^CKH = ^DAH + ^CBH. Kết hợp với AD // BC suy ra ^DKC = ^BHA = 900
=> Điểm K thuộc đường tròn (I). Mà AB vuông góc IK tại K nên (I) tiếp xúc AB (*)
+) Chứng minh nếu (I) đường kính CD tiếp xúc với AB thì AD // BC:
Ta gọi tiếp điểm giữa (I) và AB là K, qua K kẻ đường thẳng song song với AH cắt CD tại C'
Lúc này, ^KC'I = ^AHD = ^ABH. Ta có KC' // AH; AH vuông góc BH => KC' vuông góc BH
Do KI vuông góc AB nên ^IKC' = ^ABH. Suy ra ^KC'I = ^IKC' => \(\Delta\)KIC' cân tại I
=> IC' = IK = IC. Mà C và C' nằm cùng phía so với IK nên C trùng C'.
Từ đây ^KCH = ^AHI = ^KBH => Tứ giác KHCB nội tiếp. Hoàn toàn tương tự, tứ giác AKHD nội tiếp
Vậy thì ^HCB = ^HKA = 1800 - ^ADH => AD // BC (**)
+) Qua (*) và (**), ta thu được ĐPCM.
Đúng 0
Bình luận (0)
Bài 3.Cho hình thang ABCD (AB // CD) có AD = CD và AC vuông góc BC. Từ C kẻ đường thẳng song song với AD và cắt AB tại E. a) Chứng minh tứ giác AECD là hình thoi. b) Chứng minh tứ giác BEDC là hình bình hành. c) Chứng minh tam giác CEB cân. d) Giả sử tam giác CEB đều. Chứng minh tứ giác ABCD là hình thang cân
Cho tứ giác ABCD có ABCD( AB không song song với CD). Gọi E,F,G,H theo thứ tự là trung điểm của các cạnh BC, AC, AD, BD1. Tứ giác EFGH là hình gì2. Nếu AB vuông góc với CD và AB 8cm. Tính diện tích tứ giác EFGH3. Đường thẳng FH cắt AB tại M và CD tại N. Từ B kẻ đường thẳng song song với MN, cắt đường thẳng CD tại D. Chứng minh BNMPgiúp mình với ạ mình cần gấp 🙏
Đọc tiếp
Cho tứ giác ABCD có AB=CD( AB không song song với CD). Gọi E,F,G,H theo thứ tự là trung điểm của các cạnh BC, AC, AD, BD
1. Tứ giác EFGH là hình gì
2. Nếu AB vuông góc với CD và AB= 8cm. Tính diện tích tứ giác EFGH
3. Đường thẳng FH cắt AB tại M và CD tại N. Từ B kẻ đường thẳng song song với MN, cắt đường thẳng CD tại D. Chứng minh BN=MP
giúp mình với ạ mình cần gấp 🙏
1: Xét ΔCAB có
F,E lần lượt là trung điểm của CA,CB
=>FE là đường trung bình của ΔCAB
=>FE//AB và FE=AB
2
Xét ΔDAB có
G,H lần lượt là trung điểm của DA,DB
=>GH là đường trung bình của ΔDAB
=>GH//AB và GH=AB
2
GH//AB
FE//AB
Do đó: GH//FE
Ta có: GH=AB2
F
E
=
A
B
2
Do đó: GH=FE
Xét tứ giác EFGH có
GH=FE
GH//FE
Do đó: EFGH là hình bình hành
2: AB=CD
mà AB=8cm
nên CD=8cm
Xét ΔADC có
G,F lần lượt là trung điểm của AD,AC
=>GF là đường trung bình của ΔADC
=>GF//DC và
G
F
=
D
C
2
=
4
c
m
GF//DC
DC
⊥
AB
Do đó: GF
⊥
AB
Ta có: GF
⊥
AB
AB//GH
Do đó: GH
⊥
GF
Xét hình bình hành GHEF có GH
⊥
GF
nên GHEF là hình chữ nhật
=>
S
G
H
E
F
=
G
H
⋅
G
F
=
A
B
2
⋅
C
D
2
=
4
⋅
4
=
16
(
c
m
2
)
Đúng 0
Bình luận (0)
1: Xét ΔCAB có
F,E lần lượt là trung điểm của CA,CB
=>FE là đường trung bình của ΔCAB
=>FE//AB và \(FE=\dfrac{AB}{2}\)
Xét ΔDAB có
G,H lần lượt là trung điểm của DA,DB
=>GH là đường trung bình của ΔDAB
=>GH//AB và \(GH=\dfrac{AB}{2}\)
GH//AB
FE//AB
Do đó: GH//FE
Ta có: \(GH=\dfrac{AB}{2}\)
\(FE=\dfrac{AB}{2}\)
Do đó: GH=FE
Xét tứ giác EFGH có
GH=FE
GH//FE
Do đó: EFGH là hình bình hành
2: AB=CD
mà AB=8cm
nên CD=8cm
Xét ΔADC có
G,F lần lượt là trung điểm của AD,AC
=>GF là đường trung bình của ΔADC
=>GF//DC và \(GF=\dfrac{DC}{2}=4cm\)
GF//DC
DC\(\perp\)AB
Do đó: GF\(\perp\)AB
Ta có: GF\(\perp\)AB
AB//GH
Do đó: GH\(\perp\)GF
Xét hình bình hành GHEF có GH\(\perp\)GF
nên GHEF là hình chữ nhật
=>\(S_{GHEF}=GH\cdot GF=\dfrac{AB}{2}\cdot\dfrac{CD}{2}=4\cdot4=16\left(cm^2\right)\)
Đúng 1
Bình luận (0)






















