Cho y=mx2-2mx-3m-2 tính m khi :
Đồ thị hàm số có đỉnh thuộc đường đường thẳng y=3x-1
Cho hàm số bậc nhất \(y=\left(2m-1\right)x-3m+5\) có đồ thị hàm số là đường thẳng (d)
a) Vẽ đồ thị hàm số khi m = 2
b) Tìm m để (d) song song với đường thẳng (\(d_1\)) : \(y=-3x+2\)
c) Tìm m để (d) cắt đường thẳng (\(d_1\)) : \(y=-3x+2\) tại 1 điểm nằm trên trục tung
a) Khi m =2 thì y = 3x - 1
(Bạn tự vẽ tiếp)
b) Để \((d)//(d_{1})\) thì \(\begin{cases} 2m-1=-3\\ -3m+5\neq2 \end{cases} \) ⇔ \(\begin{cases} m=-1\\ m\neq1 \end{cases} \) ⇔ \(m=-1\)
c)
Để \((d) ⋂ (d1)\) thì \(2m-1\neq-3 \) ⇔ \(m\neq-1\)
Giao điểm của 2 đường thẳng thuộc trục tung => x=0
Khi đó, ta có: \(y=-3.0+2=2\)
⇒ Điểm \((0;2)\) cũng thuộc đường thẳng (d)
⇒ \(2=(2m-1).0-3m+5\) ⇔ \(m=1\) (TM)
1. Chứng minh phương trình x4 + (m2-m)x3 +mx2 - 2mx -2 = 0 luôn có nghiệm thuộc khoảng (0;2) với mọi giá trị của tham số m.
2. Cho hàm số y = \(\dfrac{x+1}{x-1}\) có đồ thị (C). Tìm tất cả giá trị của tham số m để đường thẳng (d): y = 2x + m cắt (C) tại hai điểm phân biệt mà hai tiếp tuyến của (C) tại hai điểm đó song song với nhau.
3. Chứng minh rằng với mọi giá trị của tham số m thì phương trình \(x^4+mx^3-4x^2-mx+1=0\) luôn có nghiệm trên khoảng (0;1).
4. Cho hàm số: y = \(\dfrac{1}{3}x^3-\left(m+1\right)x^2+\left(2m+4\right)x-3\) có đồ thị (Cm) (với m là tham số). Tìm m để trên đồ thị (Cm) có hai điểm phân biệt có hoành độ cùng dấu và tiếp tuyến của (Cm) tại mỗi điểm đó vuông góc với đường thẳng d: \(x+3y-6=0\)
5. Cho hàm số y = \(\dfrac{x+1}{x-2}\) có đồ thị (C); đường tròn (T) có tâm I(2;-5) và đi qua điểm E(3;-1). Tìm toạ độ các điểm M thuộc đồ thị (C) để tiếp tuyến của (C) tại M cắt đường tròn (T) tại hai điểm A, B sao cho tam giác EAB vuông tại E.
Toi mới làm được câu 2 thoi à :( Mấy câu còn lại để rảnh nghĩ thử coi sao
\(PTHDGD:\dfrac{x+1}{x-1}=2x+m\Leftrightarrow x+1=\left(2x+m\right)\left(x-1\right)\)
\(\Leftrightarrow x+1=2x^2-2x+mx-m\Leftrightarrow2x^2+\left(m-3\right)x-m-1=0\)
De ton tai 2 diem phan biet \(\Leftrightarrow\Delta>0\Leftrightarrow\left(m-3\right)^2+8m+8>0\Leftrightarrow m^2+2m+17>0\Leftrightarrow\left(m+1\right)^2+16>0\forall x\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{3-m}{2}\\x_1x_2=\dfrac{-m-1}{2}\end{matrix}\right.\)
Vi 2 tiep tuyen tai 2 diem x1, x2 song song voi nhau
\(\Rightarrow f'\left(x_1\right)=f'\left(x_2\right)\)
\(f'\left(x\right)=\dfrac{x-1-x-1}{\left(x-1\right)^2}=-\dfrac{2}{\left(x-1\right)^2}\)
\(\Rightarrow\dfrac{1}{\left(x_1-1\right)^2}=\dfrac{1}{\left(x_2-1\right)^2}\Leftrightarrow x_1^2-2x_1+1=x_2^2-2x_2+1\)
\(\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)-2\left(x_1-x_2\right)=0\Leftrightarrow\left(x_1-x_2\right)\left(x_1+x_2-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=x_2\left(loai\right)\\x_1+x_2=2\end{matrix}\right.\Leftrightarrow\dfrac{3-m}{2}=2\Leftrightarrow m=-1\)
tìm m để đồ thị hàm số \(y=mx^2-2mx-m^2-1\) (m ≠ 0) có đỉnh nằm trên đường thẳng y = x - 2
\(y=mx^2-2mx-m^2-1\)
\(=m\left(x^2-2x\right)-m^2-1\)
Điểm cố định của (d) có tọa độ là:
\(\left\{{}\begin{matrix}x^2-2x=0\\y=-m^2-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x\left(x-2\right)=0\\y=-m^2-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{0;2\right\}\\y=-m^2-1\end{matrix}\right.\)
TH1: x=0
Thay x=0 và \(y=-m^2-1\) vào y=x-2, ta được:
\(-m^2-1=0-2=-2\)
=>\(m^2+1=2\)
=>\(m^2=1\)
=>\(\left[{}\begin{matrix}m=1\\m=-1\end{matrix}\right.\)
TH2: x=2
Thay x=2 và \(y=-m^2-1\) vào y=x-2, ta được:
\(-m^2-1=2-2=0\)
=>\(m^2+1=0\)
=>\(m^2=-1\)(vô lý)
Đường thẳng nối hai điểm cực trị của đồ thị hàm số y = m x 2 + 4 - 2 m x - 6 2 x + 9 cách gốc tọa độ một khoảng lớn nhất khi m bằng
A. 1 2
B. - 1 2
C. 2
D. 1
Chọn B.
Để đồ thị có 2 điểm cực trị thì PT y ' = 0 có 2 nghiệm phân biệt. Ta tìm được điều kiện m < 0 hoặc m > 14 33 . Khi đó đường thẳng nối hai điểm cực trị có phương trình là
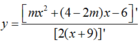
Khoảng cách từ gốc tọa độ đến đường thẳng này là
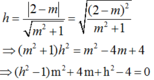 (*)
(*)
Khi h = 1 thì m = 3 4 . Khi h ≠ 1 thì (*) là phương trình bậc 2 của m. Điều kiện cần và đủ để phương trình này có nghiệm là
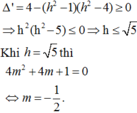
Tìm giá trị thực của tham số m để parabol (P): y = m x 2 − 2mx − 3m − 2 (m ≠ 0) có đỉnh thuộc đường thẳng y = 3x − 1.
A. m = 1
B. m = -1
C. m = - 6
D. m = 6
Cho hàm số bậc nhất y = ( 2 m – 2 ) x + m − 2 . Tìm m để hàm số có đồ thị song song với đường thẳng y = 3 x – 3 m
A. m = − 2 5
B. m = 2 5
C. m = 5 2
D. m = − 5 2
Hàm số y = ( 2 m – 2 ) x + m – 2 là hàm số bậc nhất khi 2 m – 2 ≠ 0 ⇔ m ≠ 1
Để d // d’ thì 2 m − 2 = 3 m − 3 ≠ − 3 m ⇔ m = 5 2 m ≠ 3 4 ⇔ m = 5 2 (thỏa mãn)
Vậy m = 5 2
Đáp án cần chọn là: C
Để đồ thị hàm số y = m x 2 − 2mx – m2 − 1 (m ≠ 0) có đỉnh nằm trên đường thẳng y = x − 2 thì m nhận giá trị nằm trong khoảng nào dưới đây?
A. (2; 6).
B. (− ∞ ; −2).
C. (0; 2).
D. (−2; 2).
Có bao nhiêu số thực m để đường thẳng y=-x+m cắt đồ thị hàm số y = 1 3 x 3 + 2 - m x 2 + 3 2 m - 3 x + m tại ba điểm phân biệt A(0;m), B, C sao cho đường thẳng OA là phân giác của góc BOC.
A. 1.
B. 3.
C. 2.
D. 0.
Cho hàm số \(y=\left(m-1\right)x-4\) có đồ thị là đường thẳng (d).
a) Vẽ đồ thị hàm số trên khi \(m=3\)
b) Tìm m để đường thẳng (d) song song với đường thẳng \(y=-3x+2\)
c) Tìm m để đường thẳng (d) cắt đồ thị hàm số \(y=x-7\) tại một điểm nằm bên trái trục tung
b: Để (d)//y=-3x+2 thì m-1=-3
=>m=-2
c:
PTHĐGĐ là:
(m-1)x-4=x-7
=>(m-2)x=-3
Để hai đường cắt nhau tại một điểm nằm bên trái trục tung thì m-1<>1 và -3/(m-2)<0
=>m<>2 và m-2>0
=>m>2