Các câu hỏi tương tự
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B m=0.
C.m=2.
D.m=1.
Tìm giá trị thực của tham số m để đường thẳng d: y2x+m tiếp xúc với parabol P: ym−1x2+2mx+3m−1.A.m−1.B.m0.C.m2. D.m1.
Đọc tiếp
Tìm giá trị thực của tham số m để đường thẳng d: y=2x+m tiếp xúc với parabol P: y=m−1x2+2mx+3m−1.
A.m=−1.
B.m=0.
C.m=2.
D.m=1.
Câu 1: Cho parabol (P):y=x^2+bx+c (b,c là các tham số thực)
a. Tìm giá trị của b,c biết parabol (P) đi qua điểm M(-3;2) và có trục đối xứng là đường thẳng x=-1
b. Với giá trị của b,c tìm được ở câu a), tìm m để đường thẳng d:y=-x-m cắt parabol(P) tại 2 điểm phân biệt A,B sao cho tam giác OAB vuông tại O( với O là gốc toạ độ)
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y (3m + 2)x -7m – 1 vuông góc với đường thẳng
(
∆
)
:
y
2
x
-
1
A. m 0. B. C. D.
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để đường thẳng (d): y = (3m + 2)x -7m – 1 vuông góc với đường thẳng ( ∆ ) : y = 2 x - 1
A. m = 0.
B. ![]()
C. ![]()
D. 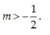
Tìm tất cả các giá trị thực của tham số m để đường thẳng d: y = (3m + 2)x − 7m − 1 vuông góc với đường △ : y = 2x − 1.
A. m = 0
B. m = - 5 6
C. m < 5 6
D. m > - 1 2
Trong phương vuông góc với Tọa độ Oxy, cho parabol (P): y = x² - 4mx + 3m² + 1, điểm A (0;3m) và đường thẳng (d): y = 2x + 3m-2 với m là tham số. Giả sử giao điểm của (d) và (P) là hai điểm M và N thì diện tích tam giác AMN bằng 4. Tìm giá trị của m
Để đồ thị hàm số y = m x 2 − 2mx – m2 − 1 (m ≠ 0) có đỉnh nằm trên đường thẳng y = x − 2 thì m nhận giá trị nằm trong khoảng nào dưới đây?
A. (2; 6).
B. (− ∞ ; −2).
C. (0; 2).
D. (−2; 2).
có bao nhiêu giá trị nguyên của tham số m thuộc (-10;10) để parabol (P): y=x^2-3x-4 không cắt đường thẳng d: y=x-m
A.1 B.3 C.4 D.2
Tìm m sao cho đường thẳng (d): y = -2x cắt Parabol (P): y = x2 -2mx+m2-1 tại hai điểm phân biệt có hoành độ lần lượt là x1, x2 sao cho biểu thức P bằng x1 bình phương cộng x2 bình phương đạt giá trị nhỏ nhất. A. m= 2 B. m=1 C. m=-2 D. m= -1










