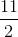Xét pt hoành độ gđ của (P) và (d) có:
\(x^2-4mx+3m^2+1=2x+3m-2\)
\(\Leftrightarrow x^2-2x\left(2m+1\right)+3m^2-3m+3=0\) (1)
Để (P) và (d) cắt nhau tại hai điểm M;N khi pt (1) có hai nghiệm pb
\(\Leftrightarrow\Delta>0\Leftrightarrow m^2+7m-2>0\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{-7+\sqrt{57}}{2}\\m< \dfrac{-7-\sqrt{57}}{2}\end{matrix}\right.\)
Gọi \(M\left(x_1;2x_1+3m-2\right);N\left(x_2;2x_2+3m-2\right)\) là hai giao điểm của (P) và (d)
\(\Rightarrow\overrightarrow{AM}\left(x_1;2x_1-2\right);\overrightarrow{AN}\left(x_2;2x_2-2\right)\)
(CT tính nhanh diện tích) \(S_{AMN}=\dfrac{1}{2}\left|x_1\left(2x_2-2\right)-x_2\left(2x_1-2\right)\right|\)\(=\dfrac{1}{2}\left|-2x_1+2x_2\right|=\left|x_2-x_1\right|=4\)
\(\Rightarrow\left(x_2-x_1\right)^2=16\)
\(\Leftrightarrow\left(x_2+x_1\right)^2-4x_1x_2=16\)\(\Leftrightarrow\left(4m+2\right)^2-4\left(3m^2-3m+3\right)=16\)
\(\Leftrightarrow4m^2+28m-24=0\)\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{-7+\sqrt{73}}{2}\\m=\dfrac{-7-\sqrt{73}}{2}\end{matrix}\right.\)(tm)
Vậy...