a, (sinx + cosx)(1 - sinx . cosx) = (cosx - sinx)(cosx + sinx)

⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx-sinx=1-sinx.cosx\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\cosx+sinx.cosx-1-sinx=0\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}sinx+cosx=0\\\left(cosx-1\right)\left(sinx+1\right)=0\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}sin\left(x+\dfrac{\pi}{4}\right)=0\\cosx=1\\sinx=-1\end{matrix}\right.\)

b, (sinx + cosx)(1 - sinx . cosx) = 2sin2x + sinx + cosx

⇔ (sinx + cosx)(1 - sinx.cosx - 1) = 2sin2x

⇔ (sinx + cosx).(- sinx . cosx) = 2sin2x

⇔ 4sin2x + (sinx + cosx) . sin2x = 0

⇔ \(\left[{}\begin{matrix}sin2x=0\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+4=0\end{matrix}\right.\)

⇔ sin2x = 0

c, 2cos³x = sin3x

⇔ 2cos³x = 3sinx - 4sin³x

⇔ 4sin³x + 2cos³x - 3sinx(sin²x + cos²x) = 0

⇔ sin³x + 2cos³x - 3sinx.cos²x = 0

Xét cosx = 0 : thay vào phương trình ta được sinx = 0. Không có cung x nào có cả cos và sin = 0 nên cosx = 0 không thỏa mãn phương trình

Xét cosx ≠ 0 chia cả 2 vế cho cos³x ta được : 

tan³x + 2 - 3tanx = 0

⇔ \(\left[{}\begin{matrix}tanx=1\\tanx=-2\end{matrix}\right.\)

d, cos²x - \(\sqrt{3}sin2x\) = 1 + sin²x

⇔ cos²x - sin²x - \(\sqrt{3}sin2x\) = 1

⇔ cos2x - \(\sqrt{3}sin2x\) = 1

⇔ \(2cos\left(2x+\dfrac{\pi}{3}\right)=1\)

⇔ \(cos\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}=cos\dfrac{\pi}{3}\)

e, cos³x + sin³x = 2cos⁵x + 2sin⁵x

⇔ cos³x (1 - 2cos²x) + sin³x (1 - 2sin²x) = 0

⇔ cos³x . (- cos2x) + sin³x . cos2x = 0

⇔ \(\left[{}\begin{matrix}sin^3x=cos^3x\\cos2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}sinx=cosx\\cos2x=0\end{matrix}\right.\)

⇔ \(\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\cos2x=0\end{matrix}\right.\)

ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)

\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)

\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)

\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)

\(\Leftrightarrow2cos^22x-2cos2x=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)

Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)

a/

\(\Leftrightarrow\frac{\sqrt{3}}{2}sin3x+\frac{1}{2}cos3x=\frac{1}{2}sinx+\frac{\sqrt{3}}{2}cosx\)

\(\Leftrightarrow sin\left(3x+\frac{\pi}{6}\right)=sin\left(x+\frac{\pi}{3}\right)\)

\(\Rightarrow\left[{}\begin{matrix}3x+\frac{\pi}{6}=x+\frac{\pi}{3}+k2\pi\\3x+\frac{\pi}{6}=\pi-x-\frac{\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+k\pi\\x=\frac{\pi}{8}+\frac{k\pi}{2}\end{matrix}\right.\)

b/

\(\Leftrightarrow2\left(\frac{1+cos2x}{2}\right)-3\sqrt{3}sin2x-4\left(\frac{1-cos2x}{2}\right)=-4\)

\(\Leftrightarrow3cos2x-3\sqrt{3}sin2x=-3\)

\(\Leftrightarrow\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x=1\)

\(\Leftrightarrow sin\left(2x-\frac{\pi}{6}\right)=1\)

\(\Leftrightarrow2x-\frac{\pi}{6}=\frac{\pi}{2}+k2\pi\)

\(\Leftrightarrow x=\frac{\pi}{3}+k\pi\)

c/

Ủa đề câu này bạn ghi đúng ko? Nhìn kì kì, cos8x hay cos3x bên vế phải vậy?

d/

\(\Leftrightarrow\frac{1}{2}cos2x-\frac{\sqrt{3}}{2}sin2x=\frac{\sqrt{3}}{2}sinx+\frac{1}{2}cosx\)

\(\Leftrightarrow cos\left(2x+\frac{\pi}{3}\right)=cos\left(x-\frac{\pi}{3}\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+\frac{\pi}{3}=x-\frac{\pi}{3}+k2\pi\\2x+\frac{\pi}{3}=\frac{\pi}{3}-x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{2\pi}{3}+k2\pi\\x=\frac{k2\pi}{3}\end{matrix}\right.\)

e/

\(\Leftrightarrow\frac{1}{2}sin8x-\frac{\sqrt{3}}{2}cos8x=\frac{\sqrt{3}}{2}sin6x+\frac{1}{2}cos6x\)

\(\Leftrightarrow sin\left(8x-\frac{\pi}{3}\right)=sin\left(6x+\frac{\pi}{6}\right)\)

\(\Rightarrow\left[{}\begin{matrix}8x-\frac{\pi}{3}=6x+\frac{\pi}{6}+k2\pi\\8x-\frac{\pi}{3}=\pi-6x-\frac{\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{28}+\frac{k\pi}{7}\end{matrix}\right.\)

a, \(sin4x.cosx-sin3x=0\)

\(\Leftrightarrow\dfrac{1}{2}sin5x+\dfrac{1}{2}sin3x-sin3x=0\)

\(\Leftrightarrow sin5x=sin3x\)

\(\Leftrightarrow\left[{}\begin{matrix}5x=3x+k2\pi\\5x=\pi-3x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\end{matrix}\right.\)

b, \(sin2x+\sqrt{3}cos2x=\sqrt{2}\)

\(\Leftrightarrow\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}cos2x=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{2}}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{4}+k2\pi\\2x+\dfrac{\pi}{3}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{24}+k\pi\\x=\dfrac{5\pi}{24}+k\pi\end{matrix}\right.\)

sin3x + 1=2sin²2x

<=> sin3x + 1 = 2\(\dfrac{1-cos4x}{2}\)

<=> sin3x + 1 = 1 - cos4x

<=> sin3x = -cos4x

<=> sin3x + cos4x = 0

<=> \(\dfrac{\sqrt{2}}{2}\)sin3x + \(\dfrac{\sqrt{2}}{2}\)cos4x = 0 (chia 2 vế cho \(\sqrt{2}\)).

<=> cos\(\dfrac{\pi}{4}\)sin3x + sin\(\dfrac{\pi}{4}\)cos4x = 0

<=> sin (3x+\(\dfrac{\pi}{4}\)) = 0

<=> sin(3x+\(\dfrac{\pi}{4}\)) = sin0

<=> \(\left[{}\begin{matrix}3x+\dfrac{\pi}{4}=0+k2\pi\\3x+\dfrac{\pi}{4}=\pi-0+k2\pi\end{matrix}\right.\)(k\(\in\)Z)

<=>\(\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+\dfrac{k2\pi}{3}\\x=\dfrac{5\pi}{12}+\dfrac{k2\pi}{3}\end{matrix}\right.\)(k\(\in\)Z)

a/ \(sin3x=sin\left(2x+x\right)=sin2xcosx+cos2x.sinx\)

\(=2sinxcos^2x+\left(1-2sin^2x\right)sinx=2sinx\left(1-sin^2x\right)+sinx-2sin^3x\)

\(=3sinx-4sin^3x\)

b/

\(tan2x+\frac{1}{cos2x}=\frac{sin2x}{cos2x}+\frac{1}{cos2x}=\frac{sin2x+1}{cos2x}=\frac{2sinxcosx+sin^2x+cos^2x}{cos^2x-sin^2x}\)

\(=\frac{\left(sinx+cosx\right)^2}{\left(sinx+cosx\right)\left(cosx-sinx\right)}=\frac{sinx+cosx}{cosx-sinx}=\frac{\left(sinx+cosx\right)\left(cosx-sinx\right)}{\left(cos-sinx\right)^2}\)

\(=\frac{cos^2x-sin^2x}{cos^2x+sin^2x-2sinxcosx}=\frac{1-2sin^2x}{1-sin2x}\)

c/

\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{cos^2x-sin^2x}\)

\(=\frac{2sinxcosx+2sinxcosx}{cos2x}=\frac{4sinxcosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)

d/

\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}=\frac{sinx}{cosx}=tanx\)

e/

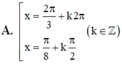
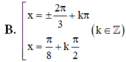
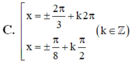
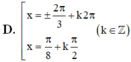
Chọn D

Ta sẽ biến đổi phương trình thành dạng tích

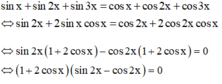
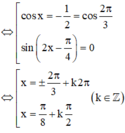
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm