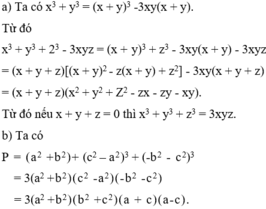phân tích đa thức thành nhân tử a2+a-3 ;;;; \(\frac{3x^2-x+1}{4x^2+2x-1}\)

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử (tách 1 hạng tử thành nhiều hạng tử)
a) a4 + a2 + 11
b) a4 + a2 - 22
c) x4 + 4x2 - 5
Lời giải:
a. Không phân tích được thành nhân tử
b. \(a^4+a^2-22=(a^2+\frac{1}{2})^2-\frac{89}{4}=(a^2+\frac{1-\sqrt{89}}{2})(a^2+\frac{1+\sqrt{89}}{2})\)
(thông thường nhân tử là số hữu tỉ, phân tích kiểu này như cố để thành nhân tử cũng không hợp lý lắm, bạn coi lại đề)
c.
$x^4+4x^2-5=(x^4-x^2)+(5x^2-5)$
$=x^2(x^2-1)+5(x^2-1)=(x^2-1)(x^2+5)=(x-1)(x+1)(x^2+5)$
Đúng 0
Bình luận (1)
Nếu sửa như bạn nói thì làm như sau:
a.
$a^4+a^2+1=(a^2+2a^2+1)-a^2=(a^2+1)^2-a^2=(a^2+1-a)(a^2+1+a)$
b.
$a^4+a^2-2=(a^4-1)+(a^2-1)=(a^2-1)(a^2+1)+(a^2-1)$
$=(a^2-1)(a^2+1+1)=(a-1)(a+1)(a^2+2)$
Đúng 0
Bình luận (1)
a2-b2-2x(a-b) phân tích đa thức thành nhân tử
\(a^2-b^2-2x\left(a-b\right)=\left(a-b\right)\left(a+b\right)-2x\left(a-b\right)=\left(a-b\right)\left(a+b-2x\right)\)
Đúng 2
Bình luận (0)
\(a^2-b^2-2x\left(a-b\right)\)
\(=\left(a-b\right)\left(a+b\right)-2x\left(a-b\right)\)
\(=\left(a-b\right)\left(a+b-2x\right)\)
Đúng 2
Bình luận (0)
phân tích đa thức thành nhân tử: (a+b)(a2-b2)+(bc)(b2-c2)+(c+a)(c2-a2)
ta có :

Hãy phân tích các đa thức sau thành nhân tử :
a) a2 + ab – 7a – 7b
b) 5ab + 4c + 20b + ac
c) a2 + 6a – b2 + 9
d) a2 – 16
a) \(a^2+ab-7a-7b=a\left(a+b\right)-7\left(a+b\right)=\left(a+b\right)\left(a-7\right)\)
b) \(5ab+4c+20b+ac=5b\left(a+4\right)+c\left(a+4\right)=\left(a+4\right)\left(5b+c\right)\)
c) \(a^2+6a-b^2+9=\left(a+3\right)^2-b^2=\left(a+b-b\right)\left(a+3+b\right)\)
d) \(a^2-16=\left(a-4\right)\left(a+4\right)\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử:
a ) x 2 + x y – x – y b ) a 2 – b 2 + 8 a + 16
a) x2 + xy –x – y = x(x + y) – (x + y) = (x + y)(x -1 ).
b) a2 – b2 + 8a + 16 = (a2 + 8a + 16) – b2 = (a + 4)2 – b2
= (a + 4 – b)(a + 4 + b).
Đúng 0
Bình luận (0)
a2−4b2−a3+ 4a2b−4ab2 phân tích đa thức thành nhân tử
phân tích đa thức thành nhân tử:
(b2 + c2 - a2 )2 - 4b2c2
\(=\left(b^2+c^2+2bc-a^2\right)\left(b^2+c^2-2bc-a^2\right)\)
\(=\left(b+c-a\right)\left(b+c+a\right)\left(b-c-a\right)\left(b-c+a\right)\)
Đúng 1
Bình luận (0)
Phân tích đa thức sau thành nhân tử: a2 – b2 – 4a + 4
a2 – b2 – 4a + 4
= a2 – 4a + 4 – b2
= (a – 2)2 – b2
= (a – 2 + b)(a – 2 – b)
= (a + b – 2)(a – b – 2)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
x2-y2+a2-b2+2ax+2by
Lời giải:
$x^2-y^2+a^2-b^2+2ax+2by=(x^2+a^2+2ax)-(y^2+b^2-2by)$
$=(x+a)^2-(y-b)^2=(x+a-y+b)(x+a+y-b)$
Đúng 1
Bình luận (0)
a) Chứng minh nếu x + y + z 0 thì
x
3
+
y
3
+
z
3
3xyz.b) Áp dụng. Phân tích các đa thức sau thành nhân tử:P
(
a
2
+
b
2
)...
Đọc tiếp
a) Chứng minh nếu x + y + z = 0 thì x 3 + y 3 + z 3 = 3xyz.
b) Áp dụng. Phân tích các đa thức sau thành nhân tử:
P = ( a 2 + b 2 ) 3 + ( c 2 - a 2 ) 3 - ( b 2 + c 2 ) 3 .