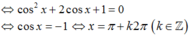Sin2 x\ 1+sinx=0
Những câu hỏi liên quan
1. 2cos2x + sinx = sin3x
2. cos2x + 2(sin3x-1)sin2(π/4 - x/2) = 0
1.
\(\Leftrightarrow2cos2x+sinx-sin3x=0\)
\(\Leftrightarrow2cos2x-2cos2x.sinx=0\)
\(\Leftrightarrow2cos2x\left(1-sinx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sinx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
Đúng 0
Bình luận (0)
2.
\(cos^2x+\left(sin3x-1\right)\left(1-cos\left(\dfrac{\pi}{2}-x\right)\right)=0\)
\(\Leftrightarrow1-sin^2x+\left(sin3x-1\right)\left(1-sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(1+sinx\right)+\left(sin3x-1\right)\left(1-sinx\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(1+sinx+sin3x-1\right)=0\)
\(\Leftrightarrow2\left(1-sinx\right)sin2x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sin2x=0\\cosx=0\end{matrix}\right.\)
\(\Leftrightarrow sin2x=0\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (1)
cho phương trình \(\dfrac{1}{sinx}+\dfrac{1}{sin2x}+\dfrac{1}{sin4x}+...+\dfrac{1}{sin2^{2018}x}=0\)
\(\dfrac{1}{sin2k}=\dfrac{sink}{sink.sin2k}=\dfrac{\left(sin2k-k\right)}{sink.sin2k}=\dfrac{sin2k.cosk-cos2k.sink}{sink.sin2k}\)
\(=\dfrac{cosk}{sink}-\dfrac{cos2k}{sin2k}=cotk-cot2k\)
Do đó pt tương đương:
\(cot\dfrac{x}{2}-cotx+cotx-cot2x+...+cot2^{2017}x-cot^{2018}x=0\)
\(\Leftrightarrow cot\dfrac{x}{2}-cot2^{2018}x=0\)
\(\Leftrightarrow\dfrac{x}{2}=2^{2018}x+k\pi\)
\(\Leftrightarrow...\)
Đúng 3
Bình luận (1)
Giải phương trình
sin
x
+
cos
x
cos
x
-
sin
x
1
+
sin
2
x
A.
x
π
/
4
+
k
π
h...
Đọc tiếp
Giải phương trình sin x + cos x cos x - sin x = 1 + sin 2 x
A. x = π / 4 + k π h o ặ c x = k π
B. x = - π / 4 + k 2 π h o ặ c x = k 2 π
C. x = - π / 4 + k π h o ặ c x = k 2 π
D. x = - π / 4 + k π h o ặ c x = k π
4sin3x+3sin2xcosx-sinx-cos3x=0cos3x+sin3x=sinx-cosx(tanx+1)sin2x=3(cosx-sinx)sinx+3sin3(x-\({ π \over 4}\))=\(\sqrt2 sinx\)
Xem chi tiết
câu 1:xét sinx=o
xét sinx khác 0
chia phương trình cho cos3x
ta được 1 phương trình mới:
4+3tanx-\(\frac{1}{sin^2x}\)-tan3x=0
<=>4+3tanx-(1+cot2x)-tan3x=0
<=>4+3tanx-1-\(\frac{1}{tan^2x}\)-tan3x=o
nhân cho tan2x ta được 1 phương trình bậc 5 với tanx
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để pt sin2 x - sinx - 3 -m = 0 có nghiệm duy nhất thuộc [-π/2;π/2]
Nghiêm của phương trình sin2 x = - sinx + 2 là:
tính giá trị biểu thức P bằng sin2-sinx*cosx+2cos2x/2sin2x-cos2x biết tan x bằng 3
Lần sau bạn vào cái hình E để gửi câu hỏi nha!
\(P=\dfrac{sin^2\alpha-sin\alpha\cdot cos\alpha+2cos^2\alpha}{2sin^2\alpha-cos^2\alpha}\)
\(P=\dfrac{tan^2\alpha-tan\alpha+2}{2tan^2\alpha-1}\) (Chia cả tử và mẫu cho \(cos^2\alpha\))
\(P=\dfrac{3^2-3+2}{2\cdot3^2-1}=\dfrac{8}{17}\)
Chúc bn học tốt!
Đúng 1
Bình luận (0)
2. CM:a1) dfrac{sin110}{cos110}+ dfrac{cos20}{sin20}0a2) sin2x + sin2(dfrac{pi}{3}-x) + sinx . sin(dfrac{pi}{3}-x) dfrac{3}{4}a3) sin2x + cos(dfrac{pi}{3}-x).cos(dfrac{pi}{3}+x) dfrac{3}{4}
Đọc tiếp
2. CM:
a1) \(\dfrac{\sin110}{\cos110}\)+ \(\dfrac{\cos20}{\sin20}\)=0
a2) sin2x + sin2(\(\dfrac{\pi}{3}\)-x) + sinx . sin(\(\dfrac{\pi}{3}\)-x)= \(\dfrac{3}{4}\)
a3) sin2x + cos(\(\dfrac{\pi}{3}\)-x).cos(\(\dfrac{\pi}{3}\)+x) = \(\dfrac{3}{4}\)
a1)\(\dfrac{sin110}{cos110}+\dfrac{cos20}{sin20}\)
\(=\dfrac{sin\left(180-70\right)}{cos\left(180-70\right)}+\dfrac{cos\left(90-70\right)}{sin\left(90-70\right)}\)
\(=\dfrac{sin70}{-cos70}+\dfrac{sin70}{cos70}=0\)
a2) \(sin^2x+sin^2\left(\dfrac{\pi}{3}-x\right)+sinx.sin\left(\dfrac{\pi}{3}-x\right)\)
\(=\dfrac{1}{2}\left(1-cos2x\right)+\dfrac{1}{2}\left[1-cos\left(\dfrac{2\pi}{3}-2x\right)\right]+\dfrac{1}{2}\left[cos\left(2x-\dfrac{\pi}{3}\right)-cos\left(\dfrac{\pi}{3}\right)\right]\)
\(=\dfrac{1}{2}-\dfrac{1}{2}.cos2x+\dfrac{1}{2}-\dfrac{1}{2}.cos\left(\dfrac{2\pi}{3}-2x\right)+\dfrac{1}{2}.cos\left(2x-\dfrac{\pi}{3}\right)-\dfrac{1}{4}\)
\(=\dfrac{3}{4}-\dfrac{1}{2}\left[cos2x+cos\left(\dfrac{2\pi}{3}-2x\right)-cos\left(2x-\dfrac{\pi}{3}\right)\right]\)
\(=\dfrac{3}{4}-\dfrac{1}{2}\left[cos2x-2.sin\dfrac{\pi}{6}.sin\left(\dfrac{\pi-4x}{2}\right)\right]\)
\(=\dfrac{3}{4}-\dfrac{1}{2}\left(cos2x-cos2x\right)\)
\(=\dfrac{3}{4}\)
a3) \(sin^2x+cos\left(\dfrac{\pi}{3}-x\right).cos\left(\dfrac{\pi}{3}+x\right)\)
\(=\dfrac{1-cos2x}{2}+\dfrac{1}{2}\left[cos\left(-2x\right)+cos\left(\dfrac{2\pi}{3}\right)\right]\)
\(=\dfrac{1-cos2x}{2}+\dfrac{cos2x}{2}-\dfrac{1}{4}\)
\(=\dfrac{1}{2}-\dfrac{1}{4}\)
\(=\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
Phương trình cos2x + sin2 x+ 2cosx +1 = 0 có nghiệm là
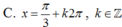
Hướng dẫn giải:
Chọn B
Ta có: cos2x + sin2x + 2cosx + 1 = 0
có 2cos2 x – 1 + 1- cos2x + 2cos x+ 1 = 0
Đúng 0
Bình luận (0)