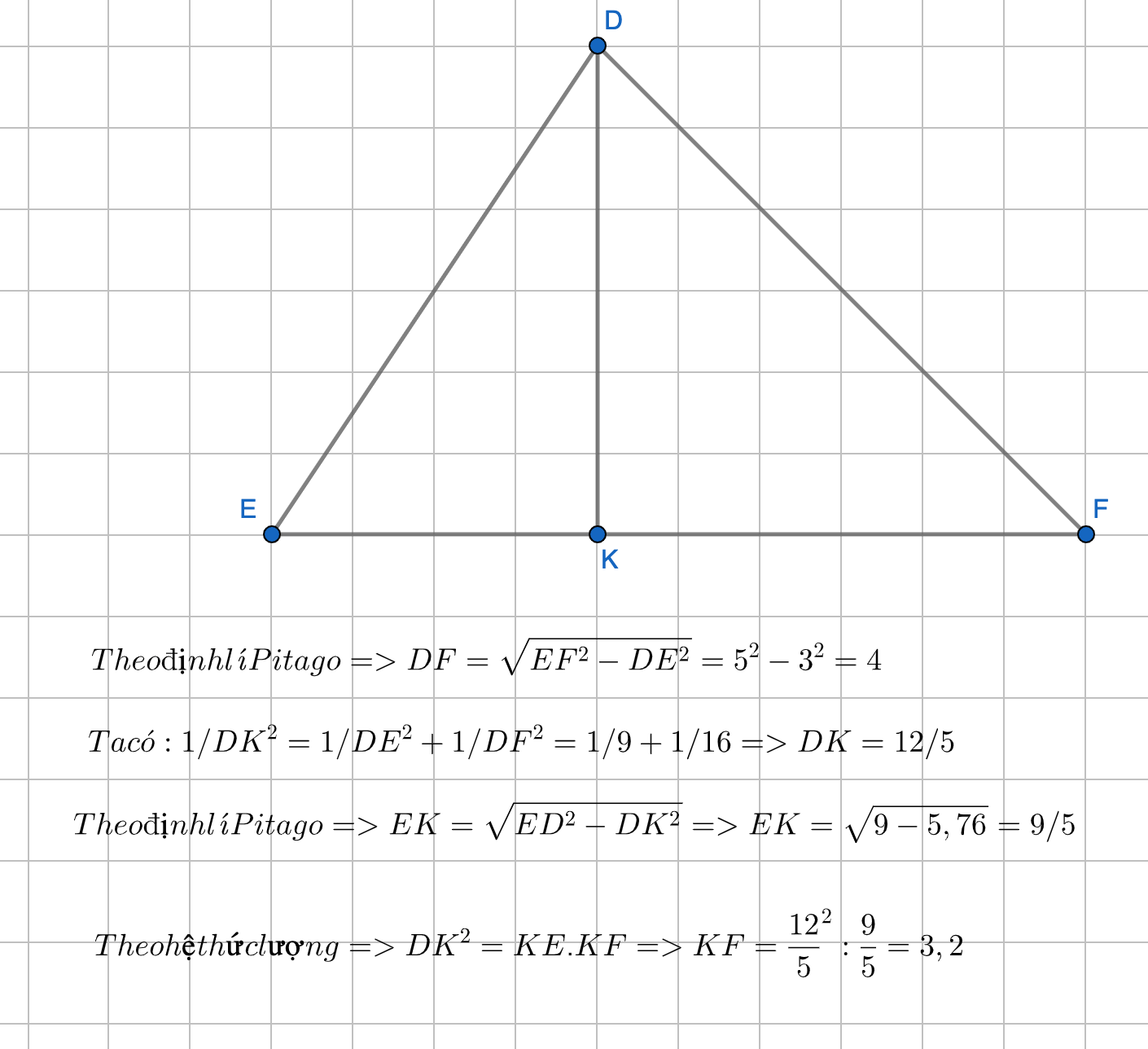
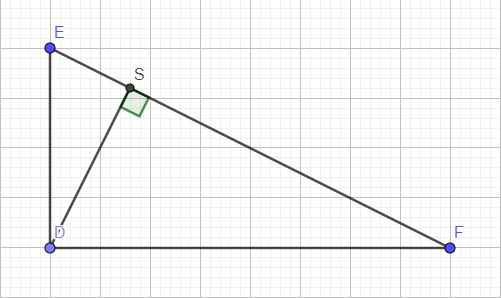
Cho tam giác DEF vuông tại D . Biết DE= 5cm; EF = 13cm. Đường phân giác góc E cắt cạnh DF tại I. Từ I kẻ đường vuông góc với EF cắt EF và ED lần lượt tại M và N
a) Tính độ dài cạnh DF
b) So sánh EI và EF
c) CM: EI vuông góc với FN
d) CM : tam giác EDI = tam giác EMI