cho a,b >0 thỏa mãn:a2+2b=4b2-a
tính giá trị biểu thức M=a2+5a+4b2-10b-4ab+2018
Những câu hỏi liên quan
Bài 6
Ạ)Cho a2 +4b2+9c2=2ab+6bc+3ca. Tính giá trị của biểu thức
A=(a-2b+1)2022+(2b-3c-1)2023+(3c-a+1)2024
B) cho x,y thỏa mãn x2+2xy+6x+6y+2y2+8=0 tìm giá trị lớn nhất và nhỏ nhất của biểu thức A= x+y+2024
Bài 6
Ạ)Cho a2 +4b2+9c2=2ab+6bc+3ca. Tính giá trị của biểu thức
A=(a-2b+1)2022+(2b-3c-1)2023+(3c-a+1)2024
B) cho x,y thỏa mãn x2+2xy+6x+6y+2y2+8=0 tìm giá trị lớn nhất và nhỏ nhất của biểu thức A= x+y+2024
A.
$a^2+4b^2+9c^2=2ab+6bc+3ac$
$\Leftrightarrow a^2+4b^2+9c^2-2ab-6bc-3ac=0$
$\Leftrightarrow 2a^2+8b^2+18c^2-4ab-12bc-6ac=0$
$\Leftrightarrow (a^2+4b^2-4ab)+(a^2+9c^2-6ac)+(4b^2+9c^2-12bc)=0$
$\Leftrightarrow (a-2b)^2+(a-3c)^2+(2b-3c)^2=0$
$\Rightarrow a-2b=a-3c=2b-3c=0$
$\Rightarrow A=(0+1)^{2022}+(0-1)^{2023}+(0+1)^{2024}=1+(-1)+1=1$
Đúng 0
Bình luận (1)
B.
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+y^2+6x+6y+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+9+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$ (do $y^2\geq 0$ với mọi $y$)
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
$\Rightarrow A_{\min}=2020; A_{\max}=2022$
Đúng 0
Bình luận (0)
Với a<2b<0, rút gọn \(\dfrac{1}{a-2b}\)√b2(a2-4ab+4b2)
\(\dfrac{1}{a-2b}.\sqrt{b^2\left(a^2-4ab+4b^2\right)}=\dfrac{1}{a-2b}.b.\left|a-2b\right|=\dfrac{1}{a-2b}.b.\left(2b-a\right)=-b\)
Đúng 0
Bình luận (0)
\(\dfrac{1}{a-2b}\cdot\sqrt{b^2\cdot\left(a^2-4ab+b^2\right)}\)
\(=\dfrac{1\cdot\left(a-2b\right)}{a-2b}\cdot b\)
=b
Đúng 0
Bình luận (0)
Cho a,b 0 thỏa mãn
a
2
+
4
b
2
12
a
b
. Xét hai mệnh đề sau
I
:
log
3
a
+
2
b
+
2
log
3
2
1
2...
Đọc tiếp
Cho a,b > 0 thỏa mãn a 2 + 4 b 2 = 12 a b . Xét hai mệnh đề sau
I : log 3 a + 2 b + 2 log 3 2 = 1 2 log 3 a + log 3 b I I : log 3 a + 2 b = 1 2 log 3 a + log 3 b
Mệnh đề nào là đúng trong các mệnh đề sau?
A. Chỉ (I)
B. Chỉ (II)
C. Cả hai sai
D. Cả hai đúng
Ta có a 2 + 4 b 2 = 12 a b ⇔ a + 2 b 2 = 16 a b
Suy ra
2 log 3 a + 2 b = log 3 2 4 + log 3 a + log 3 b ⇔ log 3 a + 2 b = 2 log 3 2 + 1 2 log 3 a + log 3 b
Do đó cả hai mệnh đề đều sai
Đáp án C
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
1) a2 - 2b - 4b2 - 4b
2) x3 + 2x2 - 2x - 1
Mong mn giúp đỡ ạ:<<<<
1: \(a^2-4b^2-2a-4b\)
\(=\left(a-2b\right)\left(a+2b\right)-2\left(a+2b\right)\)
\(=\left(a+2b\right)\left(a-2b-2\right)\)
2: \(x^3+2x^2-2x-1\)
\(=\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+3x+1\right)\)
Đúng 0
Bình luận (0)
Cho
a
0
,
b
0
thỏa mãn
a
2
+
4
b
2
5
a
b
. Khẳng định nào sau đây đúng? A.
2
log
a
+
2
b
5
log
...
Đọc tiếp
Cho a > 0 , b > 0 thỏa mãn a 2 + 4 b 2 = 5 a b . Khẳng định nào sau đây đúng?
A. 2 log a + 2 b = 5 log a + log b
B. log a + 1 + log b = 1
C. log a + 2 b 3 = log a + log b 2
D. 5 log a + 2 b = log a - log b
Cho hai số thực a và b thỏa mãn
log
a
+
3
b
+
1
a
2
+
4
b
2
+
1
+
log
4
a
b...
Đọc tiếp
Cho hai số thực a và b thỏa mãn log a + 3 b + 1 a 2 + 4 b 2 + 1 + log 4 a b + 1 a + 3 b + 1 = 2 . Khi đó giá trị của biểu thức P=6a+b là
A. 15/8
B. 25/8
C.15/4
D. 25/4
rút gọn (a+2b-c)(a+2b+c)-(a2+4b2-c2)
Lời giải:
$(a+2b-c)(a+2b+c)-(a^2+4b^2-c^2)=(a+2b)^2-c^2-a^2-4b^2+c^2$
$=(a+2b)^2-a^2-4b^2$
$=a^2+4ab+4b^2-a^2-4b^2=4ab$
Đúng 1
Bình luận (0)
\(=\left[\left(a+2b\right)^2-c^2\right]-\left(a^2+4b^2-c^2\right)\)
\(=a^2+4ab+4b^2-c^2-a^2-4b^2+c^2\)
\(=4ab\)
Đúng 0
Bình luận (0)
Cho hệ phương trình
x
2
+
2
x
y
+
8
x
3
y
2
+
12
y...
Đọc tiếp
Cho hệ phương trình x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9 x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0 có nghiệm là (a; b). Khi đó giá trị biểu thức T = 5 a 2 + 4 b 2
A. T = 24
B. T = 21
C. T = 5
D. T = 4
Điều kiện x ≥ − 7 y ≥ − 1 3 *
x 2 + 2 x y + 8 x = 3 y 2 + 12 y + 9 ( 1 ) x 2 + 4 y + 18 − 6 x + 7 − 2 x 3 y + 1 = 0 ( 2 )
Có 1 ⇔ x 2 + 2 y + 4 x − 3 y 2 − 12 y − 9 = 0 , ta coi (1) là phương trình bậc hai ẩn x và y là tham số, giải x theo y ta được x = − 3 y − 9 x = y + 1
Với x = − 3 y − 9 thì (*) ⇒ − 3 y − 9 ≥ − 7 y ≥ − 1 3 ⇔ y ≤ − 2 3 y ≥ − 1 3 (vô lí)
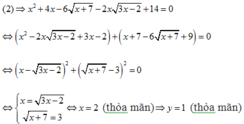
Hệ phương trình có nghiệm là 2 ; 1 ⇒ a = 2 , b = 1 ⇒ T = 24
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)