Cho tam giác ABC cân tại A.Gọi G là trọng tâm ; I là điểm nằm trong tam giác và cách đều 2 cạnh của tam giác đó.CMR 3 điểm A;G;I thẳng hàng

Những câu hỏi liên quan
Cho tam giác ABC cân tại A.Gọi G là trọng tâm,O là giao điểm của 2 đường trung trực cạnh AB,AC.chứng minh rằng :
a,tam giác BOC cân
b, ba điểm A,O,G thẳng hàng
Giúp mình nhanh lên .cảm ơn
a.tam giác ABC có O là giao điểm của 2 đường trung trực cạnh AB,AC
=>OA=OB và OA=OC
=>OB=OC=>tam giác BOC cân tại O
b.vì O là giao điểm của hai đường trung trực của tam giácABC=>AO là đương trung trực con lại của tam giác ABC
mà tam giác ABC cân tại A
=>AO đồng thời là đường trung tuyến ứng với cạnh BC của tam giác ABC mà G là trọng tâm của tam giác ABC(gt)
=>\(G\in AO\)=> ba điểm A,O,G thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A.Gọi G là trọng tâm của tam giác. Một đường thẳng d qua G cắt các cạnh AB, AC lần lượt tại E và F
CMR: 1AE2+1AF2≥9BC21AE2+1AF2≥9BC2
Giúp e với ạ cảm ơn nhiều !
Cho tam giác ABC vuông tại A.Gọi G là trọng tâm của tam giác. Một đường thẳng d qua G cắt các cạnh AB, AC lần lượt tại E và F
CMR: \(\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\ge\dfrac{9}{BC^2}\)
Giúp e với ạ cảm ơn nhiều !
cho tam giác abc cân tại a, đường cao ah, g là trọng tâm của tam giác abc. Chứng minh a, g, h thẳng hàng
(Bạn tự vẽ hình giùm)
Ta có \(\Delta ABC\)cân tại A
=> Đường cao AH cũng là đường trung tuyến của \(\Delta ABC\)
=> H nằm trên đường trung tuyến của \(\Delta ABC\)(1)
và G là trọng tâm của \(\Delta ABC\)
nên G nằm trên đường trung tuyến AH của \(\Delta ABC\)(2)
Từ (1) và (2) => A, G, H thẳng hàng (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A AM là đường cao, G là trọng tâm
Hãy chứng minh tam giác AMP=AMC
Xét \(\triangle AMB\) và \(\triangle AMC\) vuông tại `M(AM` là đường cao `)` ta có `:`
`AB=AC(` \(\triangle ABC\) cân tại `A` `)`
Chung `AM`
`=>` \(\triangle AMB = \triangle AMC\) ( 2 cạnh góc vuông )
Đúng 1
Bình luận (0)
Ta có : G là trọng tâm
=> AM là đường trung trực của BC
=> MB = MC
Xét Δ AMB và Δ AMC, có :
MB = MC (cmt)
AM là cạnh chung
\(\widehat{AMB}=\widehat{AMC}=90^o\)
=> Δ AMB = Δ AMC (c.g.c)
Đúng 1
Bình luận (0)
cho tam giác abc cân tại a có ab=ac=10cm bc=8cm gọi g là trọng tâm của tam giác abc tính ag,bg,cg
Xem chi tiết
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là giao điểm của ba đường phân giác của tam giác. Chọn câu đúng
A. Ba điểm A, G, I thẳng hàng
B. AG = GI
C. Điểm G trùng với điểm I
D. AI = 2/3 AG
cho tam giác ABC cân tại A có AD là đường phân giác . Gọi G là trọng tâm của tam giác ABC . Tính GD biết AB=13cm, BC=10cm.
xét tam giác ABD và tam giác ACD có:
AB=AC
AD(chung)
BAD=CAD(gt)
suy ra tam giác ABD=ACD(c.g.c)
suy ra _ADB=ADC mà ADC+ADB=180 suy ra ADC=ADB=180/2=90
|
-DB=DC=1/2BC=5cm
vì AD là 1 đường trung tuyến của tam giác ABC, G là trọng tâm của tam giác ABC suy ra GD=1/3AD
ta có:\(AD^2=AB^2-BD^2=13^2-5^2=169-25=144\)
\(AD=\sqrt{144}=12\left(cm\right)\)
GD=1/3AD=1/3x12=4(cm)
Đúng 1
Bình luận (0)
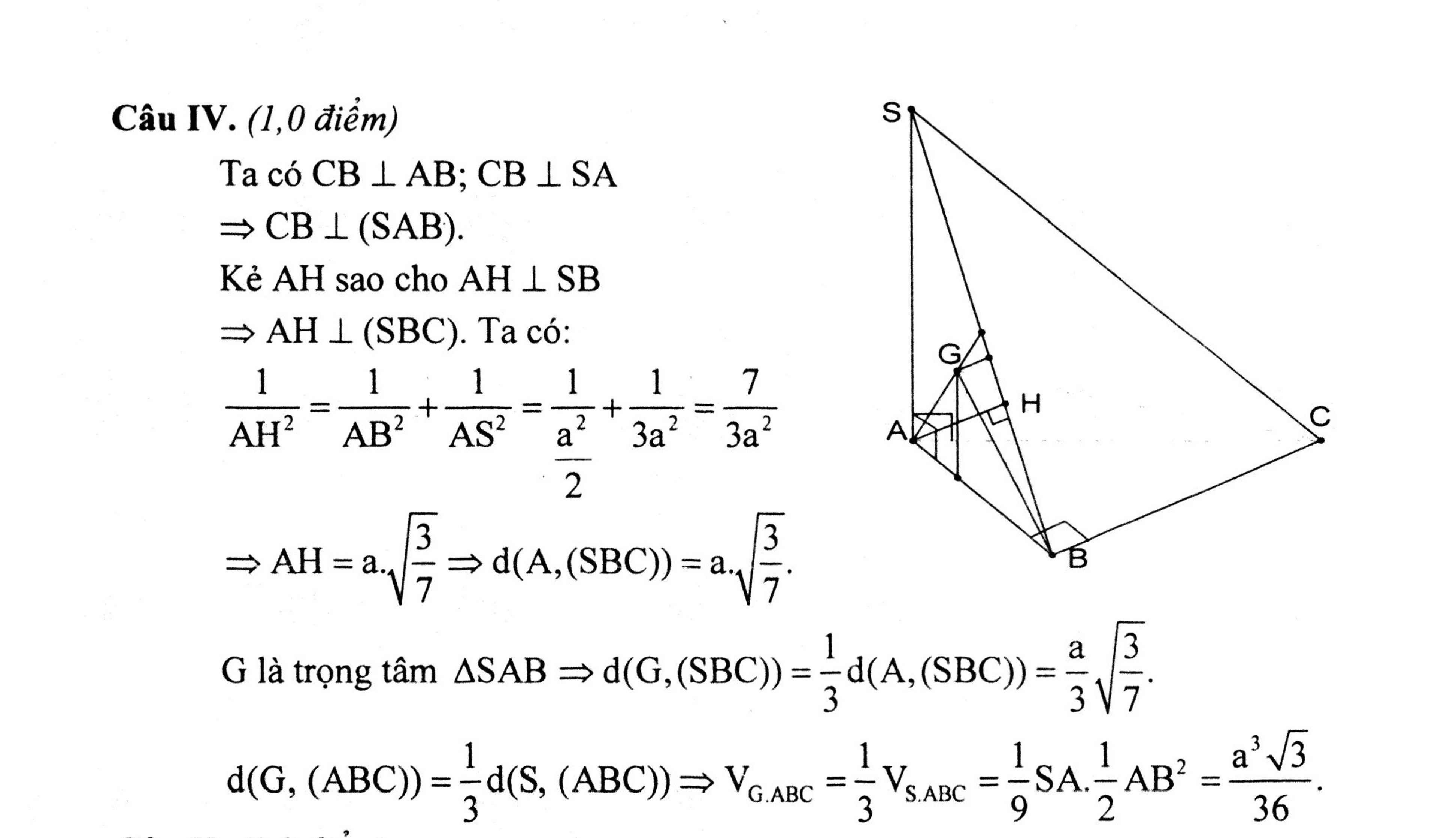
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân tại B. Cạnh AB=a . SA vuônh góc với (ABC) , SA=a căn 2 Gọi G là trọng tâm tam giác ABC. Tính (G,(SAB))