Trong tam giác ABC lấy O sao cho \(\widehat{ABO}=\widehat{ACO}\). Gọi H,K lần lượt là hình chiếu của O lên AB và AC.
a) C/m: \(OB.\sin\widehat{OAC}=OC.\widehat{OAB}\)
b) Gọi M,N lần lượt là trung điểm của BC và HK. C/m: MN vuông góc HK
cho tam giác ABC lấy điểm O sao cho \(\widehat{ABO}=\widehat{ACO}\). Gọi H và K lần lươt là hình chiếu của O trên AB, AC.
Chứng minh \(\frac{OB}{OC}=\frac{\sin\widehat{OAB}}{\sin\widehat{OAC}}\)Gọi M và N lần lươt là trung điểm của BC, HK. Chứng mih MN vuông góc HKTrong tam giác ABC lấy O sao cho góc ABO = góc ACO. Gọi H, K lần lượt là hình chiếu của O lên AB, AC. Gọi M, N lần lượt là trung điểm của BC, HK. Chứng minh MN vuông góc HK
Cho \(\Delta\)ABC điểm O nằm trong \(\Delta\) sao cho \(\widehat{ABO}=\widehat{ACO}\). Gọi H, K là hình chiếu của O trên AB, AC.
a) Gọi E, F là trung điểm OB, OC. CMR:\(\widehat{OEH}=\widehat{OFK}\).
b) CMR: MH=MK.
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB, AC.
a) Chứng minh: AE.AB = AF.AC và \(\widehat{AEF}=\widehat{ABC}\)
b) Đường trung tuyến AI của tam giác ABC cắt EF tại K. Chứng minh rằng \(cos^2B.sinB=\dfrac{KF}{BC}\)
.Ta có :
AH⊥BC,HE⊥AB→\(\widehat{AEH}=\widehat{AHB}\)
=> \(\Delta AEH\approx\Delta AHB\)(g.g)
=>\(\dfrac{AE}{AH}=\dfrac{AH}{AB}\)
=>AH\(^2\)=AE.AB
Lam tuong tu ta dc AH\(^2\)=AF.AC
=> AE.AB=AF.AC
a: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nen AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
Cho tam giác ABC cân tại A có \(\widehat A = {56^o}\)(Hình 15)
a) Tính\(\widehat B\), \(\widehat C\)
b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.
c) Chứng minh rằng MN // BC
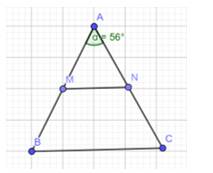
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)
Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)
b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )
Mà M, N là trung điểm của AB, AC
Nên AM = AN
Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A
\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)
c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)
Mà chúng ở vị trí đồng vị nên MN⫽BC
Cho tam giác ABC, trong tam giác lấy điểm O sao cho ABO = ACO. H,K là hình chiếu của O trên AB,AC.
a) CM: \(\frac{OB}{OC}=\frac{\sin OAB}{\sin OAC}\)
b) M,N là trung điểm của BC,KH. CM: MN vuông HK
Trong tam giác ABC lấy O sao cho góc ABO=góc ACO.Gọi H,K là hình chiếu của O trên AB,AC
a, C/m
\(\frac{OB}{OC}\)=\(\frac{\sin OAB}{\sin OAC}\)
b,M là trung điểm của BC.C/m tam giác MHK cân
Cho tam giác ABC có ba góc nhọn,AB<AC<BC.Các tia phân giác của \(\widehat{A}\)và \(\widehat{C}\)cắt nhau tại O.Gọi F và H lần lượt là hình chiếu của O trên BC và AC.Lấy I trên đoạn FC sao cho FI = AH. Gọi K là giao điểm của FH và AI.
a) C/m tam giác FCH cân và AK = KI
b) C/m B,O,K thẳng hàng

a.
Dễ thấy \(\Delta COF=\Delta COH\left(ch-cgv\right)\Rightarrow CF=CH\Rightarrow\Delta CFH\) cân tại C.
\(\Rightarrow\widehat{CFH}=\widehat{CHF}\left(1\right)\)
Kẻ \(IG//AC\left(G\in FH\right)\)
\(\Rightarrow\widehat{IGF}=\widehat{CHF}\left(2\right)\)
Từ (1);(2) \(\Rightarrow\Delta IGF\) cân tại I.\(\Rightarrow IG=FI\) mà \(FI=AH\Rightarrow GI=AH\)
Xét \(\Delta AHK\) và \(\Delta IGK\) có:
\(\widehat{HAI}=\widehat{AIG}\)
\(AH=IG\)
\(\widehat{AHG}=\widehat{HGI}\)
\(\Rightarrow\Delta AHK=\Delta IGK\left(g.c.g\right)\Rightarrow AK=KI\)
b.
Hạ \(OE\perp AB\left(E\in AB\right)\)
Do O là tâm đường tròn nội tiếp tam giác ABC nên khoảng cách từ O đến mỗi cạnh là bằng nhau.
\(\Rightarrow OE=OH=OF\)
Khi đó:
\(\Delta AOE=\Delta AOH\left(ch.cgv\right)\Rightarrow EA=HA\)
\(\Delta BOE=\Delta BOF\left(ch.cgv\right)\Rightarrow BE=BF\)
Ta có:
\(BA=BE+EA=BF+AH=BF+FI=BI\)
\(\Rightarrow\Delta ABI\) cân tại B.
Do \(KA=KI\Rightarrow BK\) trung tuyến mà BO là phân giác nên B,O,K thẳng hàng.
Cho tam giác nhọn ABC (AB<AC) nội tiếp đường trong (O). Hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Đường thẳng AH cắt BC và (O) lần lượt tại F và K (K\(\ne\)A). Gọi L là hình chiếu cuả D lên AB.
a, C/m: Tứ giác BEDC nội tiếp và BD2 = BL.
b, Gọi J là giao điểm của KD và (O) ,(J \(\ne\)K). C/m: \(\widehat{BJK}=\widehat{BDE}\)
c, Gọi I là giao điểm của BJ và ED. C/m: Tứ giác ALIJ nội tiếp và I là trung điểm của ED.
Chỉ lm bài thoii, hình bn tự vẽ nha !!!
\(a.\) Tứ giác \(BEDC\) có \(\widehat{BEC}=\widehat{BDC}=90^0\)
Suy ra tứ giác \(BEDC\) là tứ giác nội tiếp
Tam giác \(DBA\) vuông tại \(D\) có đường cao \(DL\) nên suy ra \(BD^2=BL.BA\)
\(b.\) Tứ giác \(ADEH\) có:
\(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\) nên tứ giác \(ADEH\) nội tiếp
Từ đó \(\widehat{BAK}=\widehat{BDE}\)
Mà \(\widehat{BJK}=\widehat{BAK}\) ( 2 góc nội tiếp cùng chắn một cung )
Do đó \(\widehat{BJK}=\widehat{BDE}\)
Câu c mk làm sau cho nha !