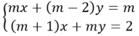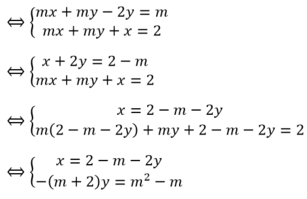Tìm m để hệ phương trình:
{2x - y = 1
{mx + 2y = 2
có nghiệm (x;y) thỏa mãn 2x - 3y = 1

Những câu hỏi liên quan
Tìm m để hệ phương trình { 3x + y = m + 1
{ x - 2y = 5m - 2
có nghiệm (x ; y) thỏa mãn 4x2 - y2 = 10
Tìm m để hệ phương trình { 3x + y = m + 1
{ x - 2y = 5m - 2
có nghiệm (x ; y) thỏa mãn 4x2 - y2 = 10
\(\left\{{}\begin{matrix}3x+y=m+1\\x-2y=5m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+2y=2m+2\\x-2y=5m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x=7m\\x-2y=5m-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=m\\m-2y=5m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m\\y=1-2m\end{matrix}\right.\\ 4x^2-y^2=10\Leftrightarrow4m^2-\left(1-2m\right)^2=10\\ \Leftrightarrow4m^2-4m^2+4m-1=10\\ \Leftrightarrow m=\dfrac{11}{4}\)
Đúng 3
Bình luận (0)
Giá trị của m để hệ phương trình
m
x
+
(
m
-
2
)
y
m...
Đọc tiếp
Giá trị của m để hệ phương trình m x + ( m - 2 ) y = m ( m + 1 ) x + m y = 2 có nghiệm duy nhất là:
![]()
![]()
![]()
![]()
Bài tập 1 Cho hệ phương trình {mx-2y-1 {2x+3y1 (1)1. Giải hệ phương trình (1) khi m 3 .2. Tìm m để hệ phương trình có nghiệm x - dfrac{1}{2} và y dfrac{2}{3} .3. Tìm nghiệm của hệ phương trình (1) theo m.
Đọc tiếp
Bài tập 1 Cho hệ phương trình {mx-2y=-1
{2x+3y=1 (1)
1. Giải hệ phương trình (1) khi m = 3 .
2. Tìm m để hệ phương trình có nghiệm x =- \(\dfrac{1}{2}\) và y =\(\dfrac{2}{3}\) ![]() .
.
3. Tìm nghiệm của hệ phương trình (1) theo m.
1: Khi m=3 thì hệ phương trình (1) trở thành:
\(\left\{{}\begin{matrix}3x-2y=-1\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{13}\\y=\dfrac{5}{13}\end{matrix}\right.\)
2: Khi x=-1/2 và y=2/3 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2\cdot\dfrac{-1}{2}+3\cdot\dfrac{2}{3}=1\\-\dfrac{1}{2}m-\dfrac{4}{3}=-1\end{matrix}\right.\Leftrightarrow m\cdot\dfrac{-1}{2}=\dfrac{1}{3}\)
hay m=-2/3
Đúng 1
Bình luận (0)
Tìm m để hệ phương trình:
{3x - 2y = 8
{mx + (m - 2)y = 5
có nghiệm (x;y) thỏa mãn 2x - y = 3
cho hệ phương trình x+y=1 và mx+2y=m. Tìm m để hệ phương trình có nghiệm duy nhất? hệ vô số nghiệm.
cho hệ phương trình mx+2y=1
2x-4y=3
tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn x-3y=7/2
Để hệ phương trình có nghiệm duy nhất thì \(\dfrac{m}{2}\ne\dfrac{2}{-4}=-\dfrac{1}{2}\)
=>\(m\ne-1\)
\(\left\{{}\begin{matrix}mx+2y=1\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2mx+4y=2\\2x-4y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\left(2m+2\right)=5\\2x-4y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\4y=2x-3=\dfrac{10}{2m+2}-3=\dfrac{10-6m-6}{2m+2}=\dfrac{-6m+4}{2m+2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{2m+2}\\y=\dfrac{-6m+4}{8m+8}=\dfrac{-3m+2}{4m+4}\end{matrix}\right.\)
x-3y=7/2
=>\(\dfrac{5}{2m+2}-\dfrac{3\cdot\left(-3m+2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+3\left(3m-2\right)}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{10+9m-6}{4m+4}=\dfrac{7}{2}\)
=>\(\dfrac{9m+4}{4m+4}=\dfrac{7}{2}\)
=>7(4m+4)=2(9m+4)
=>28m+28=18m+8
=>10m=-20
=>m=-2(nhận)
Đúng 1
Bình luận (0)
Cho hệ phương trình \(\left\{{}\begin{matrix}mx+2y=18\\x-y=-6\end{matrix}\right.\) (m là tham số). Tìm m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn \(2x+y=9\\\)
Kết hợp điều kiện đề bài và pt thứ 2 của hệ ta được:
\(\left\{{}\begin{matrix}x-y=-6\\2x+y=9\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=7\end{matrix}\right.\)
Thế vào pt đầu:
\(m.1+2.7=18\Rightarrow m=4\)
Đúng 0
Bình luận (0)
a)cho hệ phương trình \(\hept{\begin{cases}x-2y=3-m\\2x+y=3\left(m+2\right)\end{cases}}\)
Gọi nghiệm của hệ phương trình là(x;y)Tìm m để \(x^2+y^2\)đạt GTNN
b)Cho hệ phương trình \(\hept{\begin{cases}mx+y=5\\2x-y=2\end{cases}}\)
Tìm m để hệ phương trình có nghiệm thỏa mãn x+y=1