Cho parabol (P): y=x2 và đường thẳng (d): y=x+2.
Tính diện tích △AOB.

Những câu hỏi liên quan
cho hàm số y = x2 có đồ thị là parabol P và đường thẳng d: y = x + 2
1. Cminh D cắt P tại 2 điểm phân biệt A, B
2. Tính diện tích tam giác OAB
1: PTHĐGĐ là:
x^2-x-2=0
a=1; b=-1; c=-2
Vì a*c<0
nên (D) cắt (P) tại hai điểm phân biệt
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
Khi x=2 thì y=4
Khi x=-1 thì y=(-1)^2=1
=>A(2;4); B(-1;1)
2: \(OA=\sqrt{2^2+4^2}=2\sqrt{5};OB=\sqrt{\left(-1\right)^2+1^2}=\sqrt{2}\)
\(AB=\sqrt{\left(-1-2\right)^2+\left(1-4\right)^2}=3\sqrt{2}\)
Vì BA^2+BO^2=OA^2
nên ΔOAB vuông tại B
=>S BOA=1/2*BO*BA=1/2*căn 2*3*căn 2=3
Đúng 0
Bình luận (0)
Cho parabol (P) :y=1/2x^2. Vẽ (P) trên mặt phẳnv tọa độ Oxy. Bằng pp đạu số, hãy tùm tọa độ các giao điểm A và B cà đường thẳng (d):y=-x+4. Tính diện tích tam giác AOB
Cho parabol (P) :y=1/2x^2. Vẽ (P) trên mặt phẳnv tọa độ Oxy. Bằng pp đạu số, hãy tùm tọa độ các giao điểm A và B cà đường thẳng (d):y=-x+4. Tính diện tích tam giác AOB
Ta có bảng giá trị :
| \(x\) | 0 | 1 | -1 | 2 | -2 |
| \(y=\dfrac{1}{2}x^2\) | 0 | \(\dfrac{1}{2}\) | \(\dfrac{1}{2}\) | 2 | 2 |
-> \(O\left(0;0\right);C\left(1;\dfrac{1}{2}\right);D\left(-1;\dfrac{1}{2}\right);E\left(2;2\right);F\left(-2;2\right)\)
Đường cong đi qua các điểm O,C,D,E,F là đồ thị hàm số \(\left(P\right):y=\dfrac{1}{2}x^2\)
Đúng 1
Bình luận (0)
Cho parabol (P) :y=1/2x^2. Vẽ (P) trên mặt phẳnv tọa độ Oxy. Bằng pp đạu số, hãy tùm tọa độ các giao điểm A và B cà đường thẳng (d):y=-x+4. Tính diện tích tam giác AOB
Ta có bảng giá trị :
| \(x\) | 0 | 1 | -1 | 2 | -2 |
| \(y=\dfrac{1}{2}x^2\) | 0 | \(\dfrac{1}{2}\) | \(\dfrac{1}{2}\) | 2 | 2 |
-> \(O\left(0;0\right);C\left(1;\dfrac{1}{2}\right);D\left(-1;\dfrac{1}{2}\right);E\left(2;2\right);F\left(-2;2\right)\)
Đường cong đi qua các điểm O,C,D,E,F là đồ thị hàm số \(\left(P\right):y=\dfrac{1}{2}x^2\)
Xét phương trình hoành độ giao điểm chung của \(\left(P\right):y=\dfrac{1}{2}x^2\) và \(\left(d\right):y=-x+4\) là:\(\dfrac{1}{2}x^2=-x+4\\ \Leftrightarrow x^2+2x-8=0\\ \Leftrightarrow\left(x+4\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)\(\rightarrow A\left(2;2\right);B\left(-4;8\right)\)Kẻ \(AX,BY\perp Ox\)\(\rightarrow X\left(2;0\right);Y\left(-4;0\right);AX=2;BY=8\Rightarrow XY=6;OX=2;OY=4\)\(S_{XYBA}=\dfrac{\left(BY+AX\right)\cdot XY}{2}=\dfrac{\left(8+2\right)\cdot6}{2}=30\) (đvdt)\(S_{BOY}=\dfrac{BY.OY}{2}=\dfrac{8\cdot4}{2}=16\) (đvdt); \(S_{AOX}=\dfrac{AO.OX}{2}=\dfrac{2\cdot2}{2}=2\)\(\Rightarrow S_{BOA}=S_{XYBA}-S_{BOY}-S_{AOX}=30-16-2=12\) (đvdt)

Đúng 1
Bình luận (1)
Trong mặt phẳng tọa độ Oxy, cho Parabol (P):
y = x2 và đường thẳng (d): y = -x + 2
a) Tìm tọa độ giao điểm của (P) và (Q)
b) Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác OAB.
\(\left\{{}\begin{matrix}\left(P\right):y=x^2\\\left(d\right):y=-x+2\end{matrix}\right.\)
a) Tọa độ giao điểm của (P) và (Q) là nghiệm của hệ phương trình
\(\left\{{}\begin{matrix}y=x^2\\y=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2=-x+2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2+x-2=0\left(1\right)\end{matrix}\right.\)
\(pt\left(1\right)\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\) \(\left(a+b+c=1+1-2=0\right)\)
\(hpt\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=4\end{matrix}\right.\end{matrix}\right.\)
Vậy tọa độ giao điểm của (P) và (Q) là \(A\left(1;1\right)\&B\left(-2;4\right)\)
Đúng 1
Bình luận (0)
a) Phương trình hoành độ giao điểm :
x2 = - x + 2
<=> (x - 1)(x + 2) = 0
<=> \(\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Với x = 1 ta được y = 1
Với x = -2 ta được y = 4
Vậy tọa độ giao điểm là A(1; 1) ; B(-2;4)
b) Gọi C(-2 ; 0) ; D(1;0)
ta được \(S_{AOB}=S_{ABCD}-S_{BOC}-S_{AOD}\)
\(=\dfrac{\left(BC+AD\right).CD}{2}-\dfrac{BC.CO}{2}-\dfrac{AD.DO}{2}\)
\(=\dfrac{\left(4+1\right).3}{2}+\dfrac{4.2}{2}+\dfrac{1.1}{2}=12\) (đvdt)
Đúng 1
Bình luận (0)
Cho parabol (P): y=x2 và đường thẳng (d): y=mx+1 (m là tham số, x là ẩn)
Tìm giá trị của tham số m để diện tích tam giác OAB bằng 2
Tình diện tích hình phẳng giới hạn bởi parabol y = - x 2 và đường thẳng y = - x - 2
A. 2
B. 9 2
C. 1
D. 3 4
Diện tích của hình phẳng giới hạn bởi parabol y = 2 - x 2 và đường thẳng y = - x
A. 9 4
B. 9 2
C. 9
D. 18
Tình diện tích hình phẳng giới hạn bởi parabol y –x2 và đường thẳng y –x – 2. A.
2
B.
9
2
C.
1
D.
3
4
Đọc tiếp
Tình diện tích hình phẳng giới hạn bởi parabol y = –x2 và đường thẳng y = –x – 2.
A. 2
B. 9 2
C. 1
D. 3 4
Diện tích của hình phẳng giới hạn bởi parabol y = 2 - x 2 và đường thẳng y = - x là
A. S = 9 4
B. S = 9 2
C. S = 9
D. S = 18
Chọn B.
Phương pháp: Tìm hoành độ giao điểm và lấy tích phân để tích diện tích.
Cách giải: Phương trình hoành độ giao điểm là:
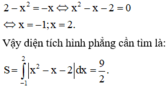
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho parabol (P): y = x 2 và đường thẳng (d): y = 2x + m (m là tham số).
b) Tìm giá trị của m để đường thẳng (d) cắt parabol (P) tại hai điểm A, B nằm về hai phía của trục tung, sao cho diện tích có diện tích gấp hai lần diện tích (M là giao điểm của đường thẳng d với trục tung).
b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
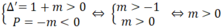
Khi đó 2 nghiệm của phương trình là:
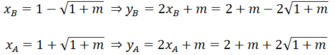
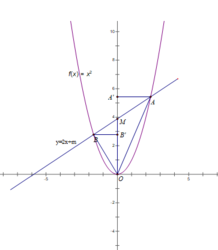
Kẻ BB' ⊥ OM ; AA' ⊥ OM
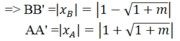
Ta có:
S A O M = 1/2 AA'.OM ; S B O M = 1/2 BB'.OM
Theo bài ra:
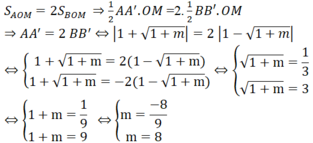
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.
Đúng 0
Bình luận (0)
















