Số nghiệm của pt log2(x+)-1=log\(\sqrt{2}\) x
Những câu hỏi liên quan
Tìm số nghiệm nguyên của bất phương trình
log
5
2
(
3
x
-
2
)
log
2
(
4
-
x...
Đọc tiếp
Tìm số nghiệm nguyên của bất phương trình log 5 2 ( 3 x - 2 ) log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0
A. 3
B. 1
C. 0
D. 2
Tích các nghiệm của phương trình
log
2
x
+
2
-
log
x
2
là A.
10
3
-
5
2
B.
10
3
+...
Đọc tiếp
Tích các nghiệm của phương trình log 2 x + 2 - log x = 2 là
A. 10 3 - 5 2
B. 10 3 + 2 2
C. 10 3 + 5 2
D. 10 3 - 2 2
Tìm tập nghiệm S của pt Log\(\sqrt{2}\) (x–1) + log\(\dfrac{1}{2}\) (x+1)=1
ĐK: x>1
\(\log_{2^{\dfrac{1}{2}}}\left(x-1\right)+\log_{2^{-1}}\left(x+1\right)=1\)
\(\log_2\left[\left(x-1\right)^2.\left(x-1\right)^{-1}\right]=\log_22\)
=> x-1 = 2(x-1)
=> x=1 (ktmđk)
Đúng 0
Bình luận (0)
câu này không cần điều kiện x>1 bạn nhé => nghiệm là x=1
Đúng 0
Bình luận (0)
giá trị của a sao cho pt log2(x+a)=3 có nghiệm là x=2 là
pt\(\left(7+4\sqrt{3}\right)^x+\left(2+\sqrt{3^{ }}\right)^x=6\)có nghiệm là
4^x-5.2^x+4=0 là
a/ \(log_2\left(2+a\right)=3\Rightarrow2+a=8\Rightarrow a=6\)
b/ Đặt \(\left(2+\sqrt{3}\right)^x=t>0\)
\(\Rightarrow t^2+t=6\Leftrightarrow t^2+t-6=0\Rightarrow\left[{}\begin{matrix}t=-3\left(l\right)\\t=2\end{matrix}\right.\)
\(\Rightarrow\left(2+\sqrt{3}\right)^x=2\Rightarrow x=log_{2+\sqrt{3}}2\)
c/ Đặt \(2^x=t>0\)
\(t^2-5t+4=0\Rightarrow\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}2^x=1\\2^x=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
4 tháng 10 2021 lúc 22:33
Tính tổng tất cả các nghiệm của phương trình: \(\dfrac{1}{2}\).log2(x+3) = log2(x+1) + x2 - x - 4 + 2\(\sqrt{x+3}\)
ĐKXĐ: \(x>-1\)
Bước quan trọng nhất là tách hàm
\(\Leftrightarrow log_2\sqrt{x+3}-2\sqrt{x+3}+\left(x+3\right)=log_2\left(x+1\right)-2\left(x+1\right)+\left(x+1\right)^2\)
Đến đây coi như xong \(\Rightarrow\sqrt{x+3}=x+1\Rightarrow x=1\)
Đúng 1
Bình luận (0)
Cho hàm số
y
ln
(
2
x
-
a
)
-
2
m
ln
(
2
x
-
a
)
+...
Đọc tiếp
Cho hàm số y = ln ( 2 x - a ) - 2 m ln ( 2 x - a ) + 2 (m là tham số thực), trong đó x, a là các số thực thỏa mãn đẳng thức
log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + log 2 ( x 2 + a 2 ) + . . . + log . . . 2 ( x 2 + a 2 ) - ( 2 n + 1 - 1 ) ( log 2 x a + 1 ) = 0
(với n là số nguyên dương). Gọi S là tập hợp các giá trị của m thoả mãn m a x [ 1 ; e 2 ] y = 1 . Số phần tử của S là
A. 0
B. 1
C. 2
D. Vô số
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)
Tìm số nghiệm của phương trình log2 x + log2 (x -1) = 2
A. 0
B. 1
C. 3
D. 2
Tìm tập nghiệm của phương trình log2(x - 2) + log2(x+1) = 2
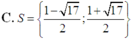
