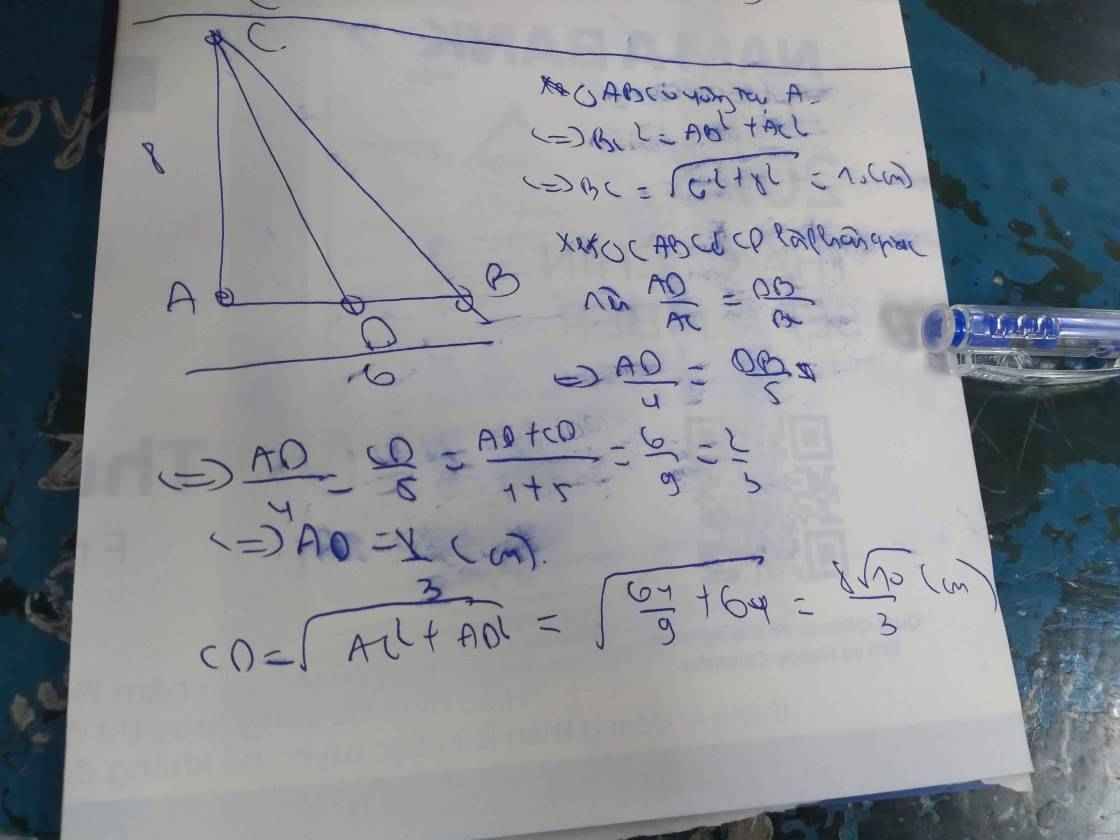
Cho tam giác ABC vuông taị A có AB = 6cm, AC = 8cm, đường phân giác AI. Tính IB và IC
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm; đường phân giác BI. Kẻ IH vuông góc BC ( H thuộc BC), gọi K là giao điểm AB và IH
Chứng minh: IB + IC + IK < 20
cho tam giác abc vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Vẽ ID vuông góc AB tại D, IE vuông góc AC tại E a) chứng minh AB+AC-BC=2AE b) cho biết AB = 6cm, AC = 8cm, tính ia ib ic
Cho tam giác ABC vuông tại A, đường cao AH. Có AB= 6cm, AC= 8cm.
a, Chứng minh tam giác AHC đồng dạng với tam giác BAC.
b, Vẽ tia phân giác của góc ABC cắt cạnh AC ở I. TÍnh độ dài AI và IC
c, Gọi K là chân đường vuông góc kẻ từ C đến tia BI. CHứng minh GÓc AKB = Góc BAH
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm, đường phân giác BI. Kẻ IH vuông góc BC ( H thuộc BC), gọi K là giao điểm của AB và IH
a) Tính BC ?
b) C/m BK = BC, từ đó suy ra BI là đường trung trực của KC
c) C/m : IB + IC + IK < 20
mình viết thêm nha !
=> tam giác BKC cân tại B
=> BO là trung trực ứng với cạnh CK
=>BI là trung trực của CK (đpcm)
Đúng 0
Bình luận (0)
Bài 1 Cho △ABC có AO là đường phân giác. Biết AB = 15cm ; AC = 25cm ; BC= 30cm. Tính OB và OC.Bài 2 Cho △ABC có vuông tại A có AI là đường phân giác. Biết AB = 5cm ; AC= 12cm. Tính IB và IC.
Bài 1:
Tam giác ABC có AO là phân giác
\(\Rightarrow\dfrac{OB}{AB}=\dfrac{OC}{AC}\)
\(\Rightarrow\dfrac{OB}{15}=\dfrac{OC}{25}\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{OB}{15}=\dfrac{OC}{25}=\dfrac{OB+OC}{15+25}=\dfrac{BC}{40}=\dfrac{30}{40}=\dfrac{3}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}OB=\dfrac{3}{4}.15=11,25\left(cm\right)\\OC=\dfrac{3}{4}.25=18,75\left(cm\right)\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Bài 1:
Xét ΔABC có
AO là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{OB}{AB}=\dfrac{OC}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{OB}{15}=\dfrac{OC}{25}\)
mà OB+OC=BC(O nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{OB}{15}=\dfrac{OC}{25}=\dfrac{OB+OC}{15+25}=\dfrac{BC}{40}=\dfrac{30}{40}=\dfrac{3}{4}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{OB}{15}=\dfrac{3}{4}\\\dfrac{OC}{25}=\dfrac{3}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}OB=\dfrac{45}{4}cm\\OC=\dfrac{75}{4}cm\end{matrix}\right.\)
Vậy: \(OB=\dfrac{45}{4}cm;OC=\dfrac{75}{4}cm\)
Bài 2:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
\(\Leftrightarrow BC=\sqrt{169}=13cm\)
Xét ΔABC có
AI là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{IB}{AB}=\dfrac{IC}{AC}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{IB}{5}=\dfrac{IC}{12}\)
mà IB+IC=BC(I nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{IB}{5}=\dfrac{IC}{12}=\dfrac{IB+IC}{5+12}=\dfrac{BC}{17}=\dfrac{13}{17}\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{IB}{5}=\dfrac{13}{17}\\\dfrac{IC}{12}=\dfrac{13}{17}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}IB=\dfrac{65}{17}cm\\IC=\dfrac{156}{17}cm\end{matrix}\right.\)
Vậy: \(IB=\dfrac{65}{17}cm;IC=\dfrac{156}{17}cm\)
Đúng 1
Bình luận (0)
Bài 2:
Tam giác ABC vuông tại A. Áp dụng Pitago
BC2 = AB2 + AC2 = 25 + 144 = 169 (cm)
=> BC = 13 (cm)
Tam giác ABC có AI là phân giác
\(\Rightarrow\dfrac{IB}{AB}=\dfrac{IC}{AC}\)
\(\Rightarrow\dfrac{IB}{5}=\dfrac{IC}{12}\)Áp dụng tính chaatd dãy tỉ số bằng nhau
\(\Rightarrow\dfrac{IB}{5}=\dfrac{IC}{12}=\dfrac{IB+IC}{5+12}=\dfrac{BC}{17}=\dfrac{13}{17}\)
\(\Rightarrow\left\{{}\begin{matrix}IB=\dfrac{13}{17}.5\approx3,8\left(cm\right)\\IC=\dfrac{13}{17}.12\approx9,2\left(cm\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Bài 1: cho tam giác ABC vuông tại A, gọi I là giao của các đường phân giác trong của tam giác.
a) Biết AB=5cm , IC=6cm. Tính BC
b) Biết IB=√ 5, IC=√ 10. Tính AB, AC.
Bài 2: cho tam giác ABC. Đường trung tuyến AD, đường cao BH, đường phân giác CE đồng quy. CMR: (BC+CA)(BC^2+CA^2-AB^2)=2BC.CA^2
Cho tam giác ABC vuông tại A , đường cao AH
a) Chứng minh ΔABC ∼ ΔABH
b)Vẽ tia phân giác AI . Tính IB và IC biết BC =10cm và AB\AC=2\3
Cho tam giác ABC vuông tại A, có AB=6cm và AC= 8cm. Tính độ dài đường phân giác trong CD
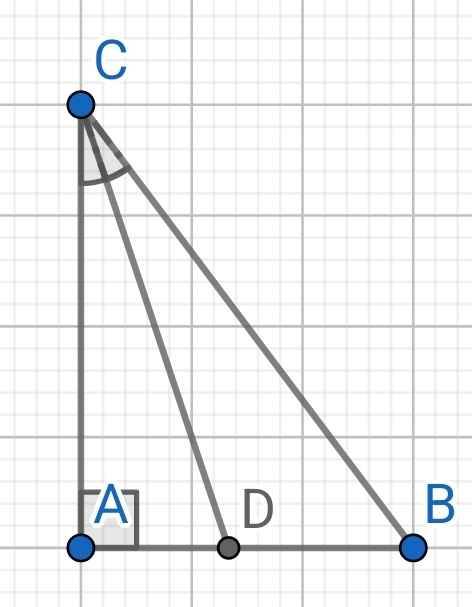∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do CD là phân giác của ∆ABC (gt)
⇒ AD/AC = BD/BC
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
AD/AC = BD/BC = (AD + BD)/(AC + BC) = AB/(AC + BC) = 6/18 = 1/3
AD/AC = 1/3 ⇒ AD = AC . 1/3 = 8/3 (cm)
∆ACD vuông tại A
⇒ CD² = AD² + AC² (Pytago)
= (8/3)² + 8²
= 640/9
⇒ CD = 8√10/3 (cm)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A , vẽ đường cao AH . Chứng minh
a)Tam giác ABC đồng dạng với tam giác ABH
b) Vẽ tia phân giác AI . Tính IB vầ IC biết BC =10cm và \(\dfrac{AB}{AC}\)=\(\dfrac{2}{3}\)
