f(x) = (3x2 – 10x + 3)(4x – 5)

+ Tam thức 3x2 – 10x + 3 có hai nghiệm x = 1/3 và x = 3, hệ số a = 3 > 0 nên mang dấu + nếu x < 1/3 hoặc x > 3 và mang dấu – nếu 1/3 < x < 3.

+ Nhị thức 4x – 5 có nghiệm x = 5/4.

Ta có bảng xét dấu:

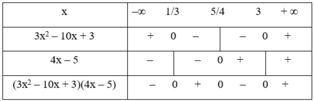
Kết luận:

f(x) > 0 khi x ∈ (1/3; 5/4) ∪ x ∈ (3; +∞)

f(x) = 0 khi x ∈ {1/3; 5/4; 3}

f(x) < 0 khi x ∈ (–∞; 1/3) ∪ (5/4; 3)

Lời giải:
$3x^3-7x+4<0$

$\Leftrightarrow (x-1)(3x^2+3x-4)<0$

Điều này xảy ra khi mà:
TH1: $x-1>0$ và $3x^2+3x-4<0$

$\Leftrightarrow x>1$ và $3x^2+3x-4<0$

Với $x>1$ thì $3x^2+3x-4> 3+3-4>0$ nên điều này không thể xảy ra.

TH2: $x-1<0$ và $3x^2+3x-4>0$

$\Leftrightarrow x<1$ và $3x^2+3x-4>0$

$\Leftrightarrow x<1$ và $(x-\frac{-3+\sqrt{57}}{6})(x-\frac{-3-\sqrt{57}}{6})>0$
$\Leftrightarrow x<1$ và ($x> \frac{-3+\sqrt{57}}{6}$ hoặc $x< \frac{-3-\sqrt{57}}{6})$

$\Leftrightarrow \frac{-3+\sqrt{57}}{6}< x< 1$ hoặc $x< \frac{-3-\sqrt{57}}{6}$

Chọn A.

Ta có: f’(x) = 3x² – 6x.

f’(x) < 0 ⇔ 3x² – 6x < 0 ⇔ 0 < x < 2.

ta có: \(\dfrac{4x^2}{3-2x}=\dfrac{9}{3-2x}\)ĐK : \(x\ne\dfrac{3}{2}\)

\(\Rightarrow4x^2-9=0\Leftrightarrow\left(2x-3\right)\left(2x+3\right)=0\Leftrightarrow x=\dfrac{3}{2}\left(ktm\right);x=-\dfrac{3}{2}\)

-> Chọn A 

Chọn B

\(1,\\ a,A=4x^2\left(-3x^2+1\right)+6x^2\left(2x^2-1\right)+x^2\\ A=-12x^4+4x^2+12x^2-6x^2+x^2=-x^2=-\left(-1\right)^2=-1\\ b,B=x^2\left(-2y^3-2y^2+1\right)-2y^2\left(x^2y+x^2\right)\\ B=-2x^2y^3-2x^2y^2+x^2-2x^2y^3-2x^2y^2\\ B=-4x^2y^3-4x^2y^2+x^2\\ B=-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^3-4\left(0,5\right)^2\left(-\dfrac{1}{2}\right)^2+\left(0,5\right)^2\\ B=\dfrac{1}{8}-\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{8}\)

\(2,\\ a,\Leftrightarrow10x-16-12x+15=12x-16+11\\ \Leftrightarrow-14x=-4\\ \Leftrightarrow x=\dfrac{2}{7}\\ b,\Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\\ \Leftrightarrow-x^3=8=-2^3\\ \Leftrightarrow x=2\\ c,\Leftrightarrow4x^2\left(4x-2\right)-x^3+8x^2=15\\ \Leftrightarrow16x^3-8x^2-x^3+8x^2=15\\ \Leftrightarrow15x^3=15\\ \Leftrightarrow x^3=1\Leftrightarrow x=1\)

\(P=x\left(2x+1\right)-x^2\left(x+2\right)+x^3-x+3\\ P=2x^2+x-x^3-2x^2+x^3-x+3\\ P=3\left(đfcm\right)\)

\(A=16x^2-y^2-16x^2+8x=8x-y^2\\ A=8\cdot3-\left(-1\right)^2=24-1=23\\ B=64x^3-80x-64x^3-1=-80x-1\\ B=-80\cdot\dfrac{1}{5}-1=-16-1=-17\)