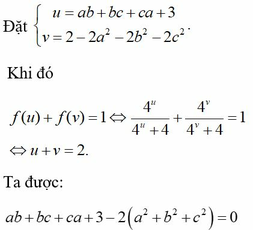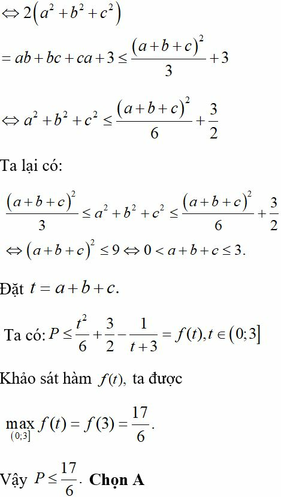Kham khảo bài lm này nhé:

\(2a^2+2b^2=5ab\\ \Leftrightarrow2a^2-5ab+2b^2=0\\ \Leftrightarrow2a^2-4ab-ab+2b^2=0\\ \Leftrightarrow2a\left(a-2b\right)+b\left(a-2b\right)=0\\ \Leftrightarrow\left(2a+b\right)\left(a-2b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=-\dfrac{b}{2}\\a=2b\end{matrix}\right.\)

Với \(a=-\dfrac{b}{2}\Leftrightarrow Q=\dfrac{-\dfrac{b}{2}+b}{-\dfrac{b}{2}-b}=\dfrac{b}{2}:\dfrac{-3b}{2}=\dfrac{b}{-3b}=-\dfrac{1}{3}\)

Với \(a=2b\Leftrightarrow Q=\dfrac{3b}{b}=3\)

\(2a^2+2b^2=5ab\)

\(\Leftrightarrow\left(2a^2-4ab\right)+\left(2b^2-ab\right)=0\)

\(\Leftrightarrow2a\left(a-2b\right)-b\left(a-2b\right)=0\)

\(\Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)

TH1: a=2b

\(Q=\dfrac{a+b}{a-b}=\dfrac{2b+b}{2b-b}=\dfrac{3b}{b}=3\)

TH2: b=2a

\(Q=\dfrac{a+b}{a-b}=\dfrac{a+2a}{a-2a}=\dfrac{3a}{-a}=-3\)

e Hoàng Phúc tui co bai tuong tu ne

M = 2(a-2ab+b) / 2(a+2ab+b) =ab/9ab = 1/9

lưu ý: a;b binh phuong nhé tui làm bieng viêt

m.n ko phải trả lời nữa,biết làm rồi

Ta có: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2+2ab+b^2\right)=9ab\Leftrightarrow\left(a+b\right)^2=\frac{9ab}{2}\)

Mặt khác: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2-2ab+b^2\right)=ab\Leftrightarrow\left(a-b\right)^2=\frac{ab}{2}\)

Do đó: \(\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\left(\frac{a+b}{a-b}\right)^2=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\Leftrightarrow M=\frac{a+b}{a-b}=\pm3\)

Mà a > b > 0 => M = 3

Ta có: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2+2ab+b^2\right)=9ab\Leftrightarrow\left(a+b\right)^2=\frac{9ab}{2}\)

Mặt khác: \(2a^2+2b^2=5ab\Leftrightarrow2\left(a^2-2ab+b^2\right)=ab\Leftrightarrow\left(a-b\right)^2=\frac{ab}{2}\)

Do đó: \(\frac{\left(a+b\right)^2}{\left(a-b\right)^2}=\left(\frac{a+b}{a-b}\right)^2=\frac{\frac{9ab}{2}}{\frac{ab}{2}}=9\Leftrightarrow M=\frac{a+b}{a-b}=\pm3\)

Mà \(a>b>0\Rightarrow M=3\)

\(2a^2+2b^2=5ab\)

<=>\(2a^2-5ab+2b^2=0\)

<=>\(2\left(a^2-\frac{5}{2}ab+b^2\right)=0\) <=> \(a^2-\frac{5}{2}ab+b^2=0\)

<=>\(a^2-2.a.\frac{5}{4}.b+b^2=0\)

<=>\(\left(a-\frac{5}{4}b\right)^2=0\) <=> \(a-\frac{5}{4}b=0\) <=> \(a=\frac{5}{4}b\)

Ta có: \(M=\frac{a+b}{a-b}=\frac{\frac{5}{4}b+b}{\frac{5}{4}b-b}=\frac{\left(\frac{5}{4}+1\right).b}{\left(\frac{5}{4}-1\right).b}=\frac{\frac{9}{4}b}{\frac{1}{4}b}=\frac{\frac{9}{4}}{\frac{1}{4}}=9\)

Vậy M=9

(*) bài này có áp dụng HĐT:\(\left(a-b\right)^2=a^2-2ab+b^2\)

\(M=a^2-a\left|a\right|-\dfrac{b}{2}\cdot2\left|b\right|-b^2\\ M=a^2+a^2-b^2-b^2\\ M=2\left(a^2-b^2\right)\\ D\)

D . \(2.\left(a^2-b^2\right)\)

chả lời câu này

 Bài này theo mình nên chọn phương án phân tích ĐTTNT từ điều kiện đầu tiên! 
2a² + 2b² = 5ab 
<=> 2a² - 5ab + 2b² = 0 
<=> 2a² - 4ab - ab + 2b² = 0 
<=> 2a(a - 2b) - b(a - 2b) = 0 
<=> (a - 2b)(2a - b) = 0 
<=> [a = 2b 
.......[ a = b/2 (Loại vì a > b) 
Thay a = 2b vào biểu thức ta có: 
. .2b + b . . .. 3b 
------------ = ---------- = 3 
. .2b - b . . . . b 

\(2\left(a^2+b^2\right)=5ab\)

\(\Leftrightarrow2a^2+2b^2-5ab=0\)

\(\Leftrightarrow\left(2a^2-4ab\right)-\left(ab-2b^2\right)=0\)

\(\Leftrightarrow2a\left(a-2b\right)-b\left(a-2b\right)=0\)

\(\Leftrightarrow\left(2a-b\right)\left(a-2b\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}a=2b\\b=2a\end{cases}}\)

Lại có : a > b > 0

=> a = 2b 

=> \(A=\frac{3a-b}{2a+b}=\frac{3.2b-b}{2.2b+b}=\frac{5b}{5b}=1\)

Vậy \(A=1\)

Ta có : 2(a² +b²) = 5ab <=> 2a² - 5ab + 2b² = 0 <=> 2a² - 4ab - ab + 2b² =0 <=> 2a(a - 2b) - b(a - 2b) =0

<=> (2a - b)(a - 2b) = 0 <=> a = 2b hay b = 2a

Vì a > b > 0 nên chỉ xảy ra trường hợp a = 2b. Do đó \(P=\frac{3.2b-b}{2.2b+b}=\frac{5b}{5b}=1\)