a=1,b=-4,c=m-1

Ta có : △ = b\(^2\)-4ac =16-4(m-2)=16-4m+8

Để PT(1) có nghiệm kép thì △=0 <=> 16-4m+8=0<=> 4m=24<=>m=6

Với m=6 PT(1) <=> x\(^2\)-4x+6-2=0<=>x\(^2\)-4x+4=0

Lại Có m=6 thì pt có nghiệm kép => x\(_1\)=x\(_2\)=-\(\dfrac{b}{2a}\)=2

Vậy Với m=6 thì pt 1 có nghiệm kép x=1

b) Theo hệ thức Vi-et 

Ta có: x\(_1\)+x\(_2\)=\(\dfrac{-b}{a}\)=4 và x\(_1\).x\(_2\)=\(\dfrac{c}{a}\)=m-2

x1\(^2\)+x2\(^2\)=9

<=> (x\(_1\)+x\(_2\))\(^2\)-2x\(_1\).x\(_2\)=9

<=>16-2m+4=9

<=>2m=1

<=> m=\(\dfrac{1}{2}\)

Vậy m =\(\dfrac{1}{2}\) thì pt(1) có 2 nghiệm thõa mãn x\(_1\)\(^2\)+ x\(_2\)\(^2\)=9

c, 

\(\Delta'=\left(m+3\right)^2-\left(m^2+3\right)\\ =m^2+6m+9-m^2-3\\ =6m+6\) 

Phương trình có nghiệm kép

\(\Delta'=0\\ 6m+6=0\\ \Leftrightarrow m=-1\) 

Với m = -1

\(\Rightarrow x^2-4x+4=0\\ \Leftrightarrow x=2\)

Bài 1:

a, Thay m=-1 vào (1) ta có:
\(x^2-2\left(-1+1\right)x+\left(-1\right)^2+7=0\\ \Leftrightarrow x^2+1+7=0\\ \Leftrightarrow x^2+8=0\left(vô.lí\right)\)

Thay m=3 vào (1) ta có:

\(x^2-2\left(3+1\right)x+3^2+7=0\\ \Leftrightarrow x^2-2.4x+9+7=0\\ \Leftrightarrow x^2-8x+16=0\\ \Leftrightarrow\left(x-4\right)^2=0\\ \Leftrightarrow x-4=0\\ \Leftrightarrow x=4\)

b, Thay x=4 vào (1) ta có:

\(4^2-2\left(m+1\right).4+m^2+7=0\\ \Leftrightarrow16-8\left(m+1\right)+m^2+7=0\\ \Leftrightarrow m^2+23-8m-8=0\\ \Leftrightarrow m^2-8m+15=0\\ \Leftrightarrow\left(m^2-3m\right)-\left(5m-15\right)=0\\ \Leftrightarrow m\left(m-3\right)-5\left(m-3\right)=0\\ \Leftrightarrow\left(m-3\right)\left(m-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=3\\m=5\end{matrix}\right.\)

c, \(\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2+7\right)=m^2+2m+1-m^2-7=2m-6\)

Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow2m-6\ge0\Leftrightarrow m\ge3\)

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=m^2+7\end{matrix}\right.\)

\(x_1^2+x_2^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-2\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-2m^2-14=0\\ \Leftrightarrow2m^2+8m-10=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-5\left(ktm\right)\end{matrix}\right.\)

\(x_1-x_2=0\\ \Leftrightarrow\left(x_1-x_2\right)^2=0\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=0\\ \Leftrightarrow\left(2m+2\right)^2-4\left(m^2+7\right)=0\\ \Leftrightarrow4m^2+8m+4-4m^2-28=0\\ \Leftrightarrow8m=28=0\\ \Leftrightarrow m=\dfrac{7}{2}\left(tm\right)\)

Bài 2:

a,Thay m=-2 vào (1) ta có:

\(x^2-2x-\left(-2\right)^2-4=0\\ \Leftrightarrow x^2-2x-4-4=0\\ \Leftrightarrow x^2-2x-8=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)

b, \(\Delta'=\left(-m\right)^2-\left(-m^2-4\right)\ge0=m^2+m^2+4=2m^2+4>0\)

Suy ra pt luôn có 2 nghiệm phân biệt

Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=-m^2-4\end{matrix}\right.\)

\(x_1^2+x_2^2=20\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=20\\ \Leftrightarrow2^2-2\left(-m^2-4\right)=20\\ \Leftrightarrow4+2m^2+8-20=0\\ \Leftrightarrow2m^2-8=0\\ \Leftrightarrow m=\pm2\)

\(x_1^3+x_2^3=56\\ \Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=56\\ \Leftrightarrow2^3-3\left(-m^2-4\right).2=56\\ \Leftrightarrow8-6\left(-m^2-4\right)-56\\ =0\\ \Leftrightarrow8+6m^2+24-56=0\\ \Leftrightarrow6m^2-24=0\\ \Leftrightarrow m=\pm2\)

\(x_1-x_2=10\\ \Leftrightarrow\left(x_1-x_2\right)^2=100\\ \Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2-100=0\\ \Leftrightarrow2^2-4\left(-m^2-4\right)-100=0\\ \Leftrightarrow4+4m^2+16-100=0\\ \Leftrightarrow4m^2-80=0\\ \Leftrightarrow m=\pm2\sqrt{5}\)

b, Để phương trình có 2 nghiệm \(\Delta\ge0\)

hay \(\left(2m+8\right)^2-4.m^2=4m^2+32m+64-4m^2=32m+64\ge0\)

\(\Leftrightarrow32m\ge64\Leftrightarrow m\ge2\)

Theo Vi et ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+8\\x_1x_2=\dfrac{c}{a}=m^2\end{matrix}\right.\)

mà \(\left(x_1+x_2\right)^2=4m^2+32m+64\Rightarrow x_1^2+x_2^2=4m^2+32m+64-2x_1x_2\)

\(=4m^2+32m+64-2m^2=2m^2+32m+64\)

Lại có : \(x_1^2+x_2^2=-2\)hay \(2m^2+32m+66=0\Leftrightarrow m=-8+\sqrt{31}\left(ktm\right);m=-8-\sqrt{31}\left(ktm\right)\)

a) Thay m=8 vào phương trình, ta được:

\(x^2-2\cdot\left(8+4\right)x+8^2=0\)

\(\Leftrightarrow x^2-24x+64=0\)

\(\text{Δ}=\left(-24\right)^2-4\cdot1\cdot64=576-256=320\)

Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{24+8\sqrt{5}}{2}=12+4\sqrt{5}\\x_2=\dfrac{24-8\sqrt{5}}{2}=12-4\sqrt{5}\end{matrix}\right.\)

Vậy: Khi m=8 thì phương trình có hai nghiệm phân biệt là \(x_1=12+4\sqrt{5};x_2=12-4\sqrt{5}\)

a, Thay m = 8 vào phương trình trên ta được : 

khi đó phương trình tương đương 

\(x^2-2\left(8+4\right)x+64=0\Leftrightarrow x^2-24x+64=0\)

Ta có : \(\Delta=\left(-24\right)^2-4.64=320>0\)

Vậy phương trình có 2 nghiệm phân biệt 

\(x_1=\dfrac{24-\sqrt{320}}{2};x_2=\dfrac{24+\sqrt{320}}{2}\)bạn tự rút gọn nhé 

1. 

xét delta có 

25 -4(-m-3)

= 25 + 4m + 12 

= 4m + 37 

để phương trình có nghiệm kép thì delta = 0 

=> 4m + 37 = 0 => m = \(\dfrac{-37}{4}\)

2. 

a) xét delta 

25 - 4(m-3) = 25 - 4m + 12 = -4m + 37 

để phương trình có nghiệm kép thì delta = 0 

=> -4m + 37 = 0 

=> m = \(\dfrac{37}{4}\)

b)

xét delta 

25 - 4(m-3) = 25 - 4m + 12 = -4m + 37 

để phương trình có 2 nghiệm phân biệt thì delta > 0 

=> -4m + 37 > 0 

=> m < \(\dfrac{37}{4}\)

4:

a: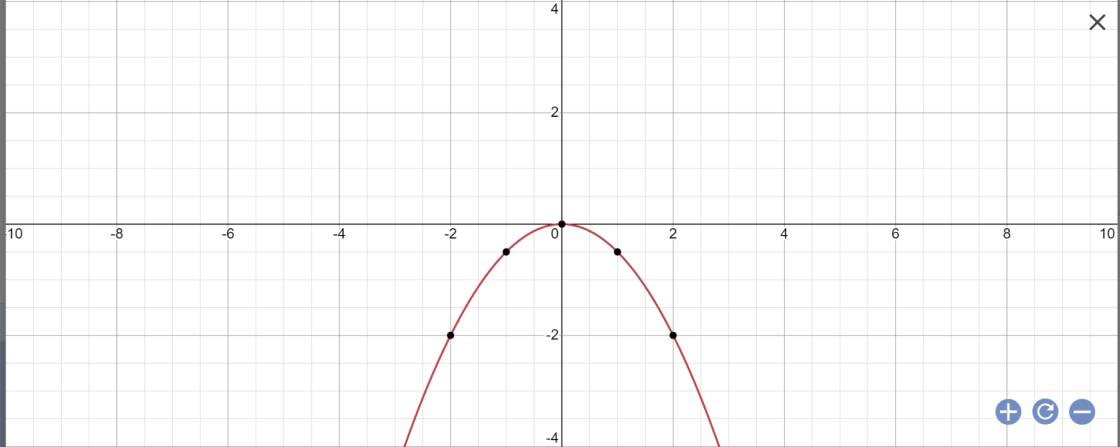 

b: Vì a=-1/2<0 nên khi x<0 thì hàm số đồng biến

Ta có: \(\Delta=4\left(m-3\right)^2-4.\left(m^2-1\right)\)

a. Để phương trình vô nghiệm thì \(\Delta< 0\Leftrightarrow\left(m-3\right)^2< m^2-1\Leftrightarrow m^2-6m+9< m^2-1\Leftrightarrow6m>10\Leftrightarrow m>\dfrac{10}{6}=\dfrac{5}{3}\)

b. Để phương trình có nghiệm thì: 

\(\Delta\ge0\Leftrightarrow\left(m-3\right)^2\ge m^2-1\Leftrightarrow m^2-6m+9\ge m^2-1\Leftrightarrow6m\le10\Leftrightarrow m\le\dfrac{10}{6}=\dfrac{5}{3}\)

c. Để phương trình có nghiệm kép thì:

\(\Delta=0\Leftrightarrow\left(m-3\right)^2=m^2-1\Leftrightarrow m^2-6m+9=m^2-1\Leftrightarrow6m=10\Leftrightarrow m=\dfrac{10}{6}=\dfrac{5}{3}\)

Nghiệm kép của phương trình là: \(\dfrac{-b}{2a}=\dfrac{2\left(m-3\right)}{2.1}=\dfrac{2\left(\dfrac{5}{3}-3\right)}{2}=-\dfrac{4}{3}\)

d. Để phương trình có nghiệm phân biệt thì:

\(\Delta>0\Leftrightarrow\left(m-3\right)^2>m^2-1\Leftrightarrow m^2-6m+9>m^2-1\Leftrightarrow6m< 10\Leftrightarrow m< \dfrac{10}{6}=\dfrac{5}{3}\)

a, Để pt vô nghiệm 

\(\Delta'=\left(m-3\right)^2-\left(m^2-1\right)=-6m+9+1=-6m+10< 0\Leftrightarrow m>\dfrac{5}{3}\)

b, Để pt có nghiệm 

\(\Delta'=-6m+10\ge0\Leftrightarrow m\le\dfrac{5}{3}\)

c, Để pt có nghiệm kép 

\(\Delta'=-6m+10=0\Leftrightarrow m=\dfrac{5}{3}\)

\(x_1=x_2=\dfrac{2\left(m-3\right)}{2}=m-3\)

d, Để pt có 2 nghiệm pb 

\(\Delta=-6m+10>0\Leftrightarrow m< \dfrac{5}{3}\)

a: khi m=1 thì pt sẽ là:

x^2+3x+1=0

=>\(x=\dfrac{-3\pm\sqrt{5}}{2}\)

b: Δ=(2m+1)^2-4m^2

=4m+1

Để phương trình có nghiệm kép thì 4m+1=0

=>m=-1/4

Khi m=-1/4 thì pt sẽ là:

x^2+x*(-1/4*2+1)+(-1/4)^2=0

=>x^2+1/2x+1/16=0

=>(x+1/4)^2=0

=>x+1/4=0

=>x=-1/4