2x3+ 4x2+12x-36 =0

Những câu hỏi liên quan
Gỉai các phương trình sau;
a, 3x2 - 8x2 - 2x + 3 = 0
b, x3 - 4x2 + 7x - 6 = 0
c, 2x3 + 7x2 + 7x + 2 = 0
d, 2x3 - 9x + 2 = 0
e, 8x3 - 4x2 + 10x - 5 = 0
a, 3x2 - 8x2 - 2x+3=0
2x(3-8) - 2x+3=0
2x5 - 2x+3=0
2x5 - 2x=0-3=
2x5 - 2x=-3
2x(5-x)=-3
5-x=-3/2
5-x=1,5
x=5-1,5
x=3,5
Đúng 0
Bình luận (0)
3,5 nha bn
chúc bn học tốt
happy new year
Đúng 0
Bình luận (0)
tìm x
x6 +2x3+1=0
x(x-5)=4x-20
x4-2x2=8-4x2
(x3-x2)-4x2+8x-4=0
\(x^6+2x^3+1=0\)
\(\Leftrightarrow\left(x^3\right)^2+2x^3+1=0\)
\(\Leftrightarrow\left(x^3+1\right)^2=0\)
\(\Leftrightarrow x^3=\left(-1\right)^3\)
\(\Leftrightarrow x=-1\)
___________
\(x\left(x-5\right)=4x-20\)
\(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
_____________
\(x^4-2x^2=8-4x^2\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(4x^2-8\right)=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+4\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x^2-2\right)\left(x^2+4\right)=0\)
\(\Leftrightarrow x^2=2\)
\(\Leftrightarrow x=\pm\sqrt{2}\)
_______________
\(\left(x^3-x^2\right)-4x^2+8x-4\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
phân tích thành nhân tử:
a, (ab-1)2 +( a+b)2 x3 + 2x2 + 2x + 1;
c, x3 - 4x2 + 12x - 27; x4 - 2x3 + 2x -1
d, x4 +2x3+ 2x2 +2x + 1 x2-2x-4y2-4y
e, x4 + 2x3 - 4x -4 x2(1 - x2) - 4 - 4x2
f, (1 + 2x) (1-2x) - x(x+2)(x-2) x2 + y2 - x2y2 + xy- x - y
Bài 1:phân tích đa thức thành nhân tửa)x2-2x-4y2-4y e)x4+2x3+2x2+2x+1b)x3+2x2+2x+1 f)x5+x4+x3+x2+x+1c)x3-4x2+12x-27d)a6-a4+2a3+2a2Làm chi tiết giúp mình với ạ, cảm ơn
Đọc tiếp
Bài 1:phân tích đa thức thành nhân tử
a)x2-2x-4y2-4y e)x4+2x3+2x2+2x+1
b)x3+2x2+2x+1 f)x5+x4+x3+x2+x+1
c)x3-4x2+12x-27
d)a6-a4+2a3+2a2
Làm chi tiết giúp mình với ạ, cảm ơn
a) \(x^2-2x-4y^2-4y=\left(x^2-4y^2\right)-\left(2x+4y\right)=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)=\left(x+2y\right)\left(x-2y-2\right)\)
b) \(x^3+2x^2+2x+1=\left(x+1\right)\left(x^2-x+1\right)+2x\left(x+1\right)=\left(x+1\right)\left(x^2-x+1+2x\right)=\left(x+1\right)\left(x^2+x+1\right)\)
c) \(x^3-4x^2+12x-27=x^3-3x^2-x^2+3x+9x-27=x^2\left(x-3\right)-x\left(x-3\right)+9\left(x-3\right)=\left(x-3\right)\left(x^2-x+9\right)\)
d) \(a^6-a^4+2a^3+2a^2=a^2\left(a^4-a^2+2a+2\right)=a^2\left[a^2\left(a-1\right)\left(a+1\right)+2\left(a+1\right)\right]=a^2\left(a+1\right)\left(a^3-a^2+2\right)=a^2\left(a+1\right)\left[a^3+a^2-2a^2+2\right]=a^2\left(a+1\right)\left[a^2\left(a+1\right)-2\left(a-1\right)\left(a+1\right)\right]=a^2\left(a+1\right)^2\left(a^2-2a+2\right)\)
Đúng 2
Bình luận (0)
a) Ta có: \(x^2-2x-4y^2-4y\)
\(=\left(x^2-4y^2\right)-\left(2x+4y\right)\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
b) Ta có: \(x^3+2x^2+2x+1\)
\(=\left(x^3+1\right)+2x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-x+1\right)+2x\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+x+1\right)\)
Đúng 1
Bình luận (0)
d) Ta có: \(a^6-a^4+2a^3+2a^2\)
\(=a^2\left(a^4-a^2+2a+2\right)\)
\(=a^2\left[a^2\left(a^2-1\right)+\left(2a+2\right)\right]\)
\(=a^2\left[a^2\left(a-1\right)\left(a+1\right)+2\left(a+1\right)\right]\)
\(=a^2\cdot\left(a+1\right)\left(a^3-a+2\right)\)
c) Ta có: \(x^3-4x^2+12x-27\)
\(=\left(x^3-27\right)-\left(4x^2-12x\right)\)
\(=\left(x-3\right)\left(x^2+3x+9\right)-4x\left(x-3\right)\)
\(=\left(x-3\right)\left(x^2-x+9\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
a/ 4x3 – xy2
b/ 5x3 – 10x2 + 5x
c/4x2 +24x+36-4y2
d/ 4x2y2 - 8xy2 + 4y2
e/ x3y + 10x2y + 35xy
f/2x3 –4x2y+2xy2–8x
g/3x2 –9xy–6x+18y
h/ x2y2 – 3xy2 + 2xy – 6y
a: \(4x^3-xy^2\)
\(=x\left(4x^2-y^2\right)\)
\(=x\left(2x-y\right)\left(2x+y\right)\)
b: \(5x^3-10x^2+5x\)
\(=5x\left(x^2-2x+1\right)\)
\(=5x\left(x-1\right)^2\)
c: \(4x^2+24x+36-4y^2\)
\(=4\left(x^2+6x+9-y^2\right)\)
\(=4\left(x+3-y\right)\left(x+3+y\right)\)
Đúng 2
Bình luận (2)
a) \(4x^3-xy^2=x\left(4x^2-y^2\right)=x\left(2x-y\right)\left(2x+y\right)\)
b) \(5x^3-10x^2+5x=5x\left(x^2-2x+1\right)=5x\left(x-1\right)^2\)
c) \(4x^2+24x+36-4y^2=\left(2x+6\right)^2-4y^2=\left(2x+6-2y\right)\left(2x+6+2y\right)\)
d) \(4x^2y^2-8xy^2+4y^2=4y^2\left(x^2-2x+1\right)=4y^2\left(x-1\right)^2\)
e) \(x^3y+10x^2y+35xy=xy\left(x^2+10x+35\right)\)
f) \(2x^3-4x^2y+2xy^2-8x=2x\left(x^2-2xy+y^2-4\right)=2x\left[\left(x-y\right)^2-4\right]=2x\left(x-y-2\right)\left(x-y+2\right)\)
g) \(3x^2-9xy-6x+18y=3x\left(x-2\right)-9y\left(x-2\right)=3\left(x-2\right)\left(x-3y\right)\)
h) \(x^2y^2-3xy^2+2xy-6y=xy\left(xy+2\right)-3y\left(xy+2\right)=\left(xy+2\right)\left(xy-3y\right)\)
Đúng 0
Bình luận (0)
g: \(3x^2-9xy-6x+18y\)
\(=3x\left(x-3y\right)-6\left(x-3y\right)\)
\(=3\left(x-2\right)\left(x-3y\right)\)
h: \(x^2y^2-3xy^2+2xy-6y\)
\(=xy^2\left(x-3\right)+2y\left(x-3\right)\)
\(=y\left(xy+2\right)\left(x-3\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tổng các nghiệm của phương trình
4
x
2
−
12
x
−
5
4
x
2
−
12
x
+
11
+
15
0
bằng: A.
5
4
B. 3 C. -3 D.
−
5
4
Đọc tiếp
Tổng các nghiệm của phương trình 4 x 2 − 12 x − 5 4 x 2 − 12 x + 11 + 15 = 0 bằng:
A. 5 4
B. 3
C. -3
D. − 5 4
Vì: 4 x 2 − 12 x + 11 = 4 x − 3 2 2 + 2 > 0 , ∀ x nên phương trình xác định với mọi x
Đặt 4 x 2 − 12 x + 11 = t ( t ≥ 2 )
⇔ 4 x 2 − 12 x + 1 = t 2 ⇔ 4 x 2 − 12 x + 15 = t 2 + 4
Khi đó, phương trình trở thành: t 2 − 5 t + 4 = 0 ⇔ t = 1 ( k t m ) t = 4 ( k t m )
Với t = 4 ⇔ 4 x 2 − 12 x + 11 = 16 ⇔ 4 x 2 − 12 x − 5 = 0
Tổng 2 nghiệm của phương trình là: 3
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Chứng minh phương trình sau vô nghiệm với mọi x:
x4 - 2x3 + 4x2 - 3x + 2 = 0
\(x^4-2x^3+4x^2-3x+2=0\\ \Leftrightarrow x^4-2x^3+x^2+3x^2-3x+2=0\\ \Leftrightarrow x^2\left(x^2-2x+1\right)+\left(3x^2-3x+2\right)=0\\ \Leftrightarrow x^2\left(x-1\right)^2+\left(3x^2-3x+2\right)=0\)
Vì \(x^2\left(x-1\right)^2\ge0\) và dễ dàng chứng minh được \(3x^2-3x+2>0\) nên pt vô nghiệm
Đúng 1
Bình luận (0)
Bài 1: phân tích đa thức thành nhân tửa)x2-y2-2x-2y e)x4-2x3+2x-1b)x2(x+2y)-x-2y f)x4+x3+2x2+x+1c)x3-4x2-9x+36 g)x2y+xy2+x2z+y2z+2xyzd)x4+2x3+2x-1 h)3x3-3y2-2(x-y)2Làm chi tiết giúp mình với ạ , cảm ơn
Đọc tiếp
Bài 1: phân tích đa thức thành nhân tử
a)x2-y2-2x-2y e)x4-2x3+2x-1
b)x2(x+2y)-x-2y f)x4+x3+2x2+x+1
c)x3-4x2-9x+36 g)x2y+xy2+x2z+y2z+2xyz
d)x4+2x3+2x-1 h)3x3-3y2-2(x-y)2
Làm chi tiết giúp mình với ạ , cảm ơn![]()
e) Ta có: \(x^4-2x^3+2x-1\)
\(=\left(x^4-1\right)-2x\left(x^2-1\right)\)
\(=\left(x^2+1\right)\left(x-1\right)\left(x+1\right)-2x\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x+1\right)\cdot\left(x^2-2x+1\right)\)
\(=\left(x+1\right)\cdot\left(x-1\right)^3\)
h) Ta có: \(3x^2-3y^2-2\left(x-y\right)^2\)
\(=3\left(x^2-y^2\right)-2\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
Đúng 1
Bình luận (0)
a) Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
b) Ta có: \(x^2\left(x+2y\right)-x-2y\)
\(=\left(x+2y\right)\left(x^2-1\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)
Đúng 1
Bình luận (0)
c) Ta có: \(x^3-4x^2-9x+36\)
\(=x^2\left(x-4\right)-9\left(x-4\right)\)
\(=\left(x-4\right)\left(x^2-9\right)\)
\(=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)
d) Ta có: \(x^4+2x^3+2x-1\)
\(=\left(x^2-1\right)\left(x^2+1\right)+2x\left(x^2+1\right)\)
\(=\left(x^2+1\right)\left(x^2+2x-1\right)\)
Đúng 1
Bình luận (0)
Tìm nghiệm:
a)2x4-3x3-6x2-x+2=0
b)x4-2x3+4x2-3x-1=0
Hàm số y 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình
2
x
3
-
9
x
2
+
12
x
+
m
0
có sáu nghiệm phân biệt. A.m - 5 B. -5 m- 4 C. 4 m 5 D.m -4
Đọc tiếp
Hàm số y= 2x3-9x2+ 12x có đồ thị như hình vẽ bên. Tìm tất cả các giá trị của tham số m để phương trình 2 x 3 - 9 x 2 + 12 x + m = 0 có sáu nghiệm phân biệt.
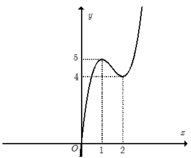
A.m< - 5
B. -5< m<- 4
C. 4< m< 5
D.m> -4
+Trước tiên từ đồ thị hàm số y= 2x3- 9x2+12x , ta suy ra đồ thị hàm số y= 2 x 3 - 9 x 2 + 12 x như hình dưới đây:
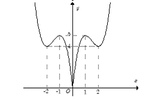
+ Phương trình 2 x 3 - 9 x 2 + 12 x + m = 0 và đường thẳng y= -m
+ Dựa vào đồ thị hàm số y = 2 x 3 - 9 x 2 + 12 x , yêu cầu bài toán trở thành:
4< -m< 5 hay -5<m< -4.
Chọn B.
Đúng 0
Bình luận (0)






















